Применение многослойных радиально-базисных нейронных сетей для верификации реляционных баз данных

Аннотация

В.В. Галушка, А.А. Молчанов, В.А. Фатхи

Предлагается интеллектуальный метод оценки достоверности данных (верификации), содержащихся в базах данных, основанный на теории искусственных нейронных сетей. Метод включает три этапа: кластеризация данных с помощью сети Кохонена, обучение радиально-базисной сети и вычисление с ее использованием оценки достоверности строк таблицы базы данных. Для создания радиально-базисных сетей и их обучения методом обратного распространения ошибки разработано программное средство. Предложенный метод верификации данных может использоваться в различных прикладных информационных системах.
Ключевые слова: базы данных, реляционная алгебра, верификация, радиально-базисные нейронные сети, обучение нейронных сетей, сети Кохонена, кластеризация.

Ключевые слова:

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

Применительно к базам данных (БД) верификация означает проверку содержащихся в ней данных на соответствие реальности, т.е. их достоверности. Необходимость такой проверки обусловлена негативными последствиями, связанными с использованием недостоверных данных.
Целью проведения верификации является повышение достоверности данных путем определения и устранения недостоверных данных. Использование такой процедуры актуально в любых прикладных информационных системах, в которых для хранения данных используется БД. Например, в [1] указывается, что в результате проведения верификации БД налоговой инспекции из неё было исключено 5 935 недостоверных записей из более чем 1 500 000.
Для определения достоверности БД требуется обладание полными знаниями, как о содержимом БД, так и о реальном мире. Система управления базами данных может контролировать только целостность БД [2], но принципиально не в состоянии контролировать достоверность БД. Контроль достоверности БД может обычно возлагается на человека, да и то в ограниченных масштабах, поскольку в ряде случаев люди не обладают полнотой знаний о реальном мире.
Основными же способами обеспечения достоверности информации БД является её входной контроль с помощью триггеров или хранимых процедур, обеспечиваемый СУБД или прикладным приложением. В случае наличия недостоверных строк в базе данных их выявление и исправление осуществляется преимущественно вручную и сопряжено с большими временными затратами.
В данной работе для определения достоверности вводимого кортежа (строки) в таблицу БД предлагается интеллектуальный метод, основанный на теории искусственных нейронных сетей [3,4], т.к. интеллектуальные информационные системы позволяют переложить на вычислительную систему часть работ традиционно выполняемых человеком.
Как известно, искусственные нейронные сети (ИНС) — это математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей. ИНС представляют собой систему соединённых и взаимодействующих между собой искусственных нейронов.
Постановка задачи. Теоретической основой реляционных БД является теория отношений [2]. Реляционная алгебра представляет собой набор таких операций над отношениями, что результат каждой из операций также является отношениям. Таким образом, верификация БД является, по сути, проверкой всех содержащихся в ней отношений или отношений, порождаемых реляционными операциями, используемыми в запросах.
Имеется БД, представляющая совокупность отношений. Рассмотрим n-арное отношение , которое является подмножеством полного декартова произведения D₁×D₂× … ×D_n множеств доменов D₁,D₂, …, D_n (n ≥ 1), не обязательно различных. Каждый элемент отношения R={r₁, r₂, …, r_j, …, r_m} (m ≥ 0) является кортежем, включающим в себя элементы множеств D₁,D₂, …, D_n : j-ый элемент отношения R равен a_j,1, a_j,2, …, aj,_n, a_j,1∈D₁, a_j,2∈D₂, ...,a_j,_n∈D_n. Отношение может быть представлено в виде таблицы (см. табл. 1), в которой столбцы (поля, атрибуты) соответствуют вхождениям доменов в отношение, а строки (записи) — наборам из n значений, взятых из исходных доменов. Каждому элементу r_j поставим в соответствие параметр d(r_j) — достоверность данного элемента такова, что 0 < d(r_j) < 1.
Рассмотрим следующий случай — имеется таблица, содержащая некоторое (относительно небольшое) количество достоверных данных, т.е. для каждого r_j∈R_d(r_j) = 1. Данная таблица постоянно пополняется. Необходимо для каждой новой строки r_m+1, заносимой в таблицу, определить её достоверность d(r_m+1) (cм. табл. 1).

Для простоты описания метода определения достоверности вводимого кортежа ограничимся проверкой отношений, содержащих только числовые данные. В случае необходимости поля строкового типа могут быть исключены или заменены числовыми кодами.
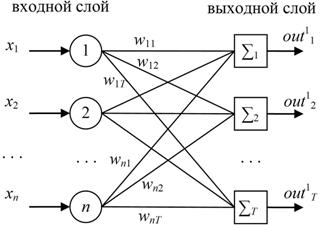
Таблица БД хранит в себе информацию о совокупности объектов предметной области принадлежащих одному классу (являющихся экземплярами одной сущности). Однако в этой совокупности могут быть выделены группы объектов похожих между собой в пределах группы, и максимально отличающихся от объектов, принадлежащих другой группе, т.е. кластеров. Первым этапом верификации является выявление этих кластеров. Для определения принадлежности элемента к кластеру используются сети Кохонена, преимущество которых заключается в обучении без учителя [4]. При этом, количество кластеров T соответствует количеству нейронов выходного слоя и определяется в соответствии с методикой, описанной в [5]. Конфигурация сети представлена на рис. 1, где x₁, x₂, …, x_n  — входные сигналы сети, n — количество элементов кортежа; w_ik — вес связи между i-ым нейроном входного слоя и k-ым нейроном выходного слоя, k = 1, 2, …, T; out¹1, out¹2, …, out¹T — значения выходов нейронов последнего слоя.

Рис. 1. Нейронная сеть Кохонена

Результатом кластеризации сетью Кохонена будет получение для каждого элемента r_i пары (r_i, C_k), где C_k — кластер, к которому принадлежит элемент r_i. Данное множество пар используется при обучении  радиально-базисной нейронной сети.
Для использования радиально-базисной нейронной сети определим количество нейронов во входном и выходном слое, количество скрытых слоев и нейронов в каждом из них, функции активации нейронов каждого слоя.
Количество нейронов во входном слое определяется количеством n столбцов анализируемой таблицы. Количество нейронов скрытого слоя определяется для каждого случая отдельно, однако проведенные ранее исследования показывают, что достаточным является количество в 1,5 – 2 раза превышающее количество нейронов в выходном слое [6]. Количество нейронов в последнем (выходном) слое соответствует количеству кластеров T, определённых на предыдущем этапе с помощью сети Кохонена. Схема применяемой радиально-базисной сети приведена на рис. 2.
Текущее состояние нейрона определяется как взвешенная сумма его входов , где x_i — значение входа, w^Lij — веса связей. При этом, для нейронов первого слоя x_i = a_ji, ,  L = 2, 3 — номер слоя, u — номер нейрона в слое.
Выход нейрона есть функция его состояния: y = f(s). Нелинейная функция f называется активационной и может иметь различный вид. Одной из наиболее распространённых является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида): f(s) = (1 + e-^αs)^-1. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции — простое выражение для ее производной: f '(s) = α f(s)(1 –  f (s)).
Производная функции активации используется при обучении сети. Для решения поставленной задачи будем использовать алгоритм обратного распространения ошибки, который предполагает два прохода по всем слоям сети: прямого и обратного. При прямом проходе входной вектор подается на входной слой нейронной сети, после чего распространяется по сети от слоя к слою. В результате генерируется набор выходных сигналов, который и является фактической реакцией сети на данный входной образ. Во время прямого прохода все синаптические веса сети фиксированы. На каждой итерации во время обратного прохода производится корректировка весов нейронной сети в соответствии с дельта-правилом: Δw_i = νδx_i , где δ — ошибка на выходе скрытого нейрона, ν — коэффициент скорости обучения, x_i — значения, поступающие по входным связям, для которых вычисляется коррекция. Зная ее величину для i-й связи, можно вычислить новый вес w_i(h + 1) = w_i(h) + Δw, где h — номер итерации обучения. Веса связей настраиваются с целью максимального приближения выходного сигнала сети к желаемому. На каждом h-ом этапе обучения

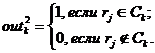
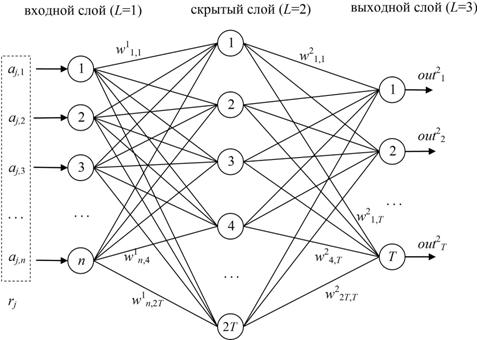
Рис. 2. Радиально-базисная сеть

В результате обучения радиально-базисной сети методом обратного распространения ошибки с использованием полученного множества пар (r_j, C_k) будет получена сеть, способная классифицировать объекты, информация о которых хранится в анализируемой таблице. Благодаря способности нейронных сетей к обобщению, т.е. распространению выделенных знаний на неизвестные ранее образцы, обученную сеть можно применять для классификации объектов, не входивших в достоверную БД. При этом степень уверенности в принадлежности образца, поданного на вход, к определённому классу определяется максимальным значением выхода нейронов выходного слоя, т.е. d(r_m+1) = max(out²1, out²2, …, out²T), где out²_i — значение выхода i-го нейрона выходного слоя сети; max — функция, вычисляющая максимальное значение; d ­­— оценка достоверности.
Низкое значение d означает, что поданный на вход образец не относится ни к одному из классов с достаточной степенью уверенности и, следовательно, может содержать ошибки или неточности. Данный параметр можно использовать в качестве значения оценки достоверности.
Таким образом, в методике можно выделить 3 основных этапа, указанных на рис. 3.

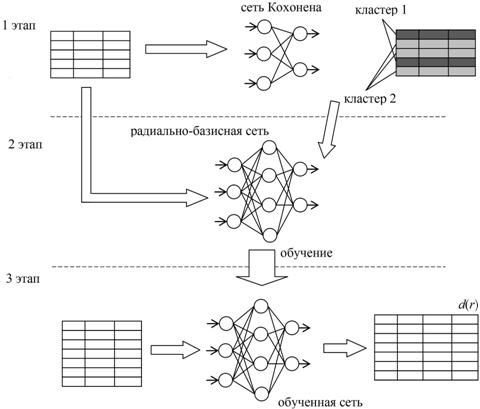
Рис. 3. Общая схема методики верификации таблицы базы данных

Помимо рассмотренного случая, возможен вариант, когда имеется таблица, содержащая большое количество строк, достоверность которых неизвестна и её требуется оценить. Данный случай можно свести к описанному ранее, если в качестве подготовительного этапа верификации выбрать из таблицы некоторое число строк и проверить их вручную, получив, таким образом, достоверные строки, которые можно использовать в качестве обучающей выборки.
Таким образом, предложенная методика может применяться для решения задач верификации различных БД. На данный момент программно реализована процедура создания радиально-базисных ИНС заданной конфигурации и их обучения методом обратного распространения ошибки с возможностью управления параметрами обучения [7]. Приведенное математическое описание методики позволяет получить её программную реализацию для дальнейшего проведения численных экспериментов и практического применения полученного программного средства.

Литература

1. 1.Открыт новый этап верификации баз данных по имущественным налогам физических лиц [Электронный ресурс]. — Сайт УФНС России по Московской области. // URL: http://www.r50.nalog.ru/ns/3869612/ (дата обращения: 20.02.2012)
   2.Карпова Т.С. Базы данных: модели, разработка, реализация [Текст] / Т.С. Карпова — СПб.: Питер, 2001. — 304 с.; ил. ISBN 5-272-00278-4
   3.Барсегян А.А. Технологии анализа данных: Data Mining, Visual Mining, Text Mining, OLAP [Текст] / А.А. Барсегян, М.С. Куприянов, М.С. Кузнецов, В.В. Степаненко, И.И. Холод. — 2-е изд. перераб. и доп. — СПб.: БХВ-Петербург, 2007. — 384 с.: ил. ISBN 5-94157-991-8
   4.Каллан Р. Основные концепции нейронных сетей [Текст].: Пер. с англ. — М.: Издательский дом «Вильямс», 2001. — 287 с. ISBN 5-8459-0210-X
   5.Галушка В.В. Методика определения оптимального числа нейронов выходного слоя сети Кохонена при решении задач кластеризации [Текст] / В.В. Галушка, Д.В. Фатхи // Информационная безопасность регионов. — 2011. — №2. — с. 41-44
   6.Галушка В.В. Программная модель для исследования возможностей применения искусственных нейронных сетей в агропромышленном комплексе [Текст] / В.В. Галушка, В.А. Фатхи // Состояние и перспективы развития сельскохозяйственного машиностроения: материалы междунар. науч.-практ. конф. / ДГТУ. — Ростов н/Д, 2011. — с. 229-231
   7.Программа синтеза многослойных искусственных нейронных сетей прямого распространения с изменяемыми параметрами обучения: свид-во о гос. регистрации прогр. для ЭВМ 2011617298 Рос. Федерация / В.В. Галушка, Дм.В. Фатхи, Д.В. Фатхи; заяв. 2011615489 21.07.2011