Математическое моделирование и компьютерная визуализации сложных геометрических форм

Аннотация

Г.С. Рачковская

Дата поступления статьи: 20.01.2013

В настоящей статье представлены математическое моделирование и возможности компьютерной визуализации сложных геометрических объектов методами компьютерной графики трансформированных (математически преобразованных) исходных хорошо известных аналитических поверхностей (базовых поверхностей). В качестве базовых использованы аналитические поверхности, такие как плоскость, конус, цилиндр, сфера, эллипсоид вращения и др. Графические возможности компьютерной визуализации сложных геометрических объектов обеспечиваются специально разработанным компьютерным приложением “ArtMathGraph” (AMG).  AMG-приложение позволяет в интерактивном режиме формировать из отдельных построенных геометрических образов компьютерные композиции, как модели сложных технических, природных или архитектурных объектов. 

Ключевые слова: математическое моделирование, аналитические поверхности, компьютерная визуализация

05.01.01 - Инженерная геометрия и компьютерная графика

Одним из эффективных методов моделирования сложных поверхностей является метод, основанный на применении математических преобразований к аналитическим представлениям исходных хорошо известных поверхностей (базовых поверхностей). Так как исходные поверхности и используемые математические преобразования содержат в своем аналитическом представлении варьируемые параметры,  то в результате комбинирования этих параметров появляется возможность получить широкий набор преобразованных поверхностей, а использование методов компьютерной композиции визуальных объектов позволяет успешно решать задачи по аналитическому и визуальному моделированию произвольных сложных геометрических форм заданного вида.
На основе аналитических поверхностей [1], таких как плоскость (1), сфера (2), конус (3), цилиндр (4),  эллипсоид вращения (5), параболоид вращения (6), однополостной гиперболоид вращения (7), гиперболический параболоид  (8), являющихся в данной работе базовыми поверхностями (рис. 1), а также на основе аналитических поверхностей, полученных в результате математических преобразований приведенных базовых поверхностей (рис. 2, 3), разработана компьютерная методика интерактивного моделирования и визуализации сложных геометрических форм технических, природных и архитектурных образов.

Рис. 1. Базовые поверхности.

Рис. 2. Производные конической поверхности.

Рис. 3. Производные цилиндрической поверхности.

          В качестве примера, для конуса и цилиндра продемонстрированы в графическом виде (рис. 2, 3)  действия некоторых математических преобразований, использованных в настоящей разработке. Действия этих математических преобразований приведены ниже в аналитическом виде на примере уравнений исходного и преобразованных конусов.
Параметрические уравнения исходного конуса (1):
                                                     
                   
Параметрические уравнения преобразованных конусов.
1. Правильная k-гранная пирамида (2):
                      
             .      
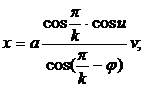
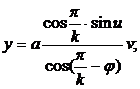
2. Конус с синусоидально преобразованной поверхностью (3):
     
      ,           
где k – кратность преобразования, d – амплитуда волновой поверхности.   
3. Конус с эпициклоидально преобразованной поверхностью (4):

 
  
      ,           
где k– количество долей на конической поверхности.     
Кроме этих трех преобразований, использованы преобразования кручения вдоль оси oz(5) и изгибания (6), а также преобразование локального (по оси oz) уширения или сужения(7), предназначенное для образования на боковой поверхности плавных выпуклых или вогнутых кольцевых областей (это преобразование построено на основе уравнения кривой “локон Аньези” [2]).
4. Преобразованная поверхность конуса кручением вдоль оси oz для граненой боковой поверхности (5):
           ,
где  x, y, z  рассчитываются по формулам для k-гранной пирамиды, а
 определяет направление и степень кручения.
5. Преобразованная поверхность конуса  изгибанием  по оси oy (6):
                ,
где x, y, zрассчитываются по формулам для исходной поверхности конуса, а  qопределяет направление и степень изгибания.
6. Преобразованная поверхность конуса локальным (по осиoz) уширением (рис. 7):
        ,
где x, y, z рассчитываются по формулам для исходной поверхности конуса,  pопределяет степень уширения, а vc определяет положение (по осиoz) локального уширения.
Результаты последовательного действия нескольких преобразований на исходную коническую поверхность показаны на рис. 2 (5, 8, 9).
Аналогичные результаты действия одного или последовательного действия нескольких математических преобразований на исходную цилиндрическую поверхность продемонстрированы в графическом виде на рис. 3.
Другие методические примеры приведены на рис. 4. Так, изгибание цилиндра позволяет получить тор, а  компьютерная композиция нескольких геометрических объектов позволяет получить, например, два сцепленных тора (рис. 4.1) или изображение сложного геометрического объекта,  состоящего, в частности, из четырех сопряженных между собой преобразованных цилиндров (рис. 4.2).

                
1                        2                       3                               4
Рис. 4. Компьютерные модели технических, природных и архитектурных форм.

       Примеры более сложных компьютерных композиций, включающих аналитическую аппроксимацию природных объектов и элементов архитектуры [3, 4], приведены на рис. 4.3 и  4.4 соответственно.
Компьютерная визуализация всех смоделированных геометрических объектов проведена с помощью ранее разработанного приложения AMG (“ArtMathGraph”) [5]. Следует подчеркнуть, что AMG-приложение основано только на методах аналитической геометрии и компьютерной графики и каждое построенное изображение имеет математическое описание, которое может быть получено в аналитическом виде.
В AMG-приложении предусмотрена возможность в интерактивном режиме формировать из отдельных построенных геометрических образов компьютерные композиции, как модели сложных технических, природных или архитектурных объектов.

Литература

1. Кривошапко С.Н., Иванов В.Н. Энциклопедия  аналитических поверхностей. - М. : Наука, 2010. - 556 с.
2. Бронштейн И.Н., Семендяев К.А.Справочник по математике.- М. :ГИТТЛ, 1964. – 608 с.
3. Kharabayev Yu.N., Rachkovskaya N.S., Rachkovskaya G.S. Development and Computer Graphics of Intricate Geometrical Forms. [Текст] // Proceedings of the International Conference on Computing, Communications and Control Technologies (CCCT 2005), Austin (Texas), USA, 2005. Vol.1, P. 42-45.   
4.  Rachkovskaya, G.S., Kharabayev, Yu.N. Towards the Construction of Artistic Visual Images by Means of Analytical Geometry and Computer Graphics. [Текст] // The Journal of Polish Society for Geometry and Engineering Graphics, Vol.16. Poland. 2006. P. 37-40. 
5. Rachkovskaya, G.S., Kharabayev, Yu.N., and Rachkovskaya, N.S. Computer composition of the transformed classical surfaces as the ways and means of the construction of visual models of realistic objects (The new software application “ArtMathGraph”). [Электронный ресурс] // Proceedings of the 15-th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision 2007, Plzen, Czech Republic, 2007. Режим доступа: http:// www.WSCG.eu (доступ свободный)  – Яз. англ.  P. 29-32.