Построение модели равнопрочной многопролетной балки
Аннотация
Дата поступления статьи: 27.03.2013Методом последовательных приближений решена задача оптимизации многопролетной неразрезной балки с сечением из сварного двутавра. Получен закон изменения ширины полки, при котором максимальные расчетные напряжения по энергетической теории прочности в каждом сечении одинаковы по всей длине. Решение выполнено численно при помощи комплекса MatLab. Для определения усилий в балке использовался метод сил. Несущая способность балки с переменной по длине жесткостью увеличилась по сравнению с балкой постоянной жесткости в 2 раза при той же массе. Предложенный метод может применяться и для рам при учете вклада продольных сил в расчетные напряжения.
Ключевые слова: многопролетная балка, метод сил, оптимизация, равнопрочность, сварной двутавр, переменная жесткость
В большинстве конструкций применяются балки с постоянными по длине размерами поперечного сечения, а для снижения расхода материала целесообразно использовать балки переменной жесткости. Оптимальной с точки зрения расхода материала является конструкция, в которой в каждом поперечном сечении максимальное напряжение постоянно и равно допускаемому [1].
Известно, что в статически определимой балке величина внутренних усилий (поперечной силы и изгибающего момента) не зависит от распределения жесткостей по ее длине. В статически неопределимых балках наоборот, изменение жесткости на каком-либо участке приводит к перераспределению усилий [6], что осложняет задачу поиска оптимальной геометрии сечения. Рассмотрим метод оптимизации неразрезных балок на примере четырехпролетной балки, загруженной равномерно распределенной нагрузкой q (рис.1). Идея используемого метода изложена в работе [2,7,8].
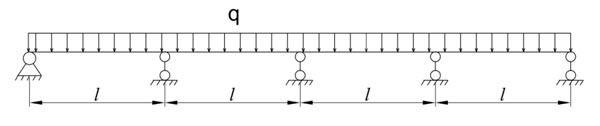
Рис.1. ‒ Неразрезная балка, загруженная распределенной нагрузкой q
Для определения усилий будем использовать метод сил. Основная система, грузовая эпюра, а также одна из единичных эпюр для рассматриваемой балки представлены на рис. 2.
Система канонических уравнений метода сил имеет вид:
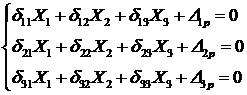
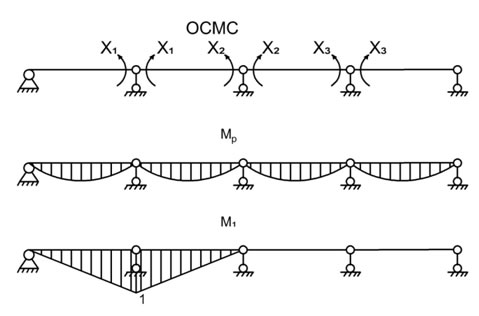
Рис.2. ‒ Основная система, грузовая и единичная эпюры метода сил.
Единичные и грузовые коэффициенты определяются по формулам Мора [4]:
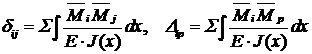 (1)
(1)
Так как момент инерции является функцией от x, то интегралы в выражениях(1) вычисляем численно при помощи формулы трапеций.
Сечение балки принимаем в виде сварного двутавра с переменной шириной полки (рис.3). Остальные размеры принимаем постоянными.
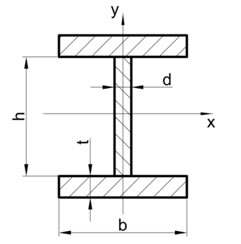
Рис. 3. ‒ Поперечное сечение сварной балки.
Геометрические характеристики такой балки определяются по формулам: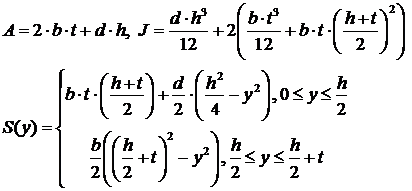
Нормальные и касательные напряжения вычисляются по формулам: 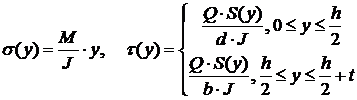
Расчетное напряжение по IV теории прочности:![]() .
.
Балка будет равнопрочной, если максимальные расчетные напряжения в каждом сечении будут одинаковыми [3,9].
Сущность предложенного метода оптимизации заключается в следующем:
- На первом этапе принимаем ширину полки b=const и вычисляем максимальные расчетные напряжения в каждом сечении.
- На втором этапе изменяем размер b пропорционально возникшим напряжениям:
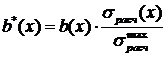 , где
, где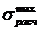 - максимальное расчетное напряжение по всей длине балки,
- максимальное расчетное напряжение по всей длине балки,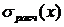 - максимальное напряжение в заданном сечении.
- максимальное напряжение в заданном сечении. - Чтобы масса балки во втором приближении осталась такой же, умножаем величину b в каждом сечении на коэффициент
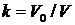 , где -
, где - 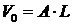 объем балки постоянного сечения,
объем балки постоянного сечения, 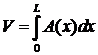 - объем балки переменного сечения.
- объем балки переменного сечения. - Процесс повторяем до тех пор, пока напряжения в предыдущем и последующем приближении отличаются более чем на 1%.
При расчетах задавались следующими исходными данными: l=6м, q=40кН/м, d = 2 см, h = 60 см, t = 3см. Полученные в результате графики изменения ширины полки b и максимальных расчетных напряжений представлены на рис.4-5. Штриховая линия на рис.5 – напряжения в балке постоянного сечения, сплошная линия – напряжения в балке переменной жесткости.
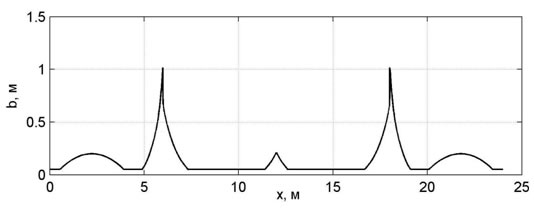
Рис.4. ‒ График изменения ширины полки
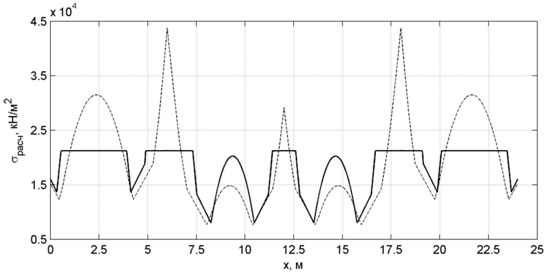
Рис.5. ‒График изменения максимальных расчетных напряжений
Максимальные расчетные напряжения для балки переменного сечения составили 213 МПа, а для балки постоянного сечения при той же массе и той же нагрузке – 437 МПа. Таким образом, можно говорить об увеличении несущей способности в 2 раза. Предложенный способ может также применяться и для рам, но при этом необходимо учитывать вклад продольных сил в расчетные напряжения [10].
Отметим, что в сварных конструкциях еще одним эффективным способом изменения сечения является изменение высоты стенки [5]. На практике используют не криволинейное очертание балки или ее поясов, а дискретную форму сечения. В разрезных сварных балках сечение обычно изменяют один раз, т.е. балку составляют из трех элементов, средний из которых проектируют по моменту в середине пролета, два крайних – по моменту в месте изменения сечения, а в балках пролетных строений автодорожных мостов сечение изменяют в 3-5 местах.
Литература:
- Андреев В.И., Потехин И.А. О равнопрочных и равнонапряженных конструкциях// Сб. тр. Воронеж, гос. арх.-строит. ун-т. 2007. С. 84-90.
- Чепурненко А.С., Языев Б.М. Оптимизация формы поперечного сечения сжатых стержней из условия устойчивости//Научное обозрение. 2012. № 6. — С. 45-49.
- Андреев В.И., Потехин И.А. Оптимизация по прочности толстостенных оболочек. М.: МГСУ, 2011. – 86 с.
- Варданян Г.С., Андреев В.И., Атаров Н.М., Горшков А.А. Сопротивление материалов с основами теории упругости и пластичности – М., Издательство АСВ, 1995. – 568 с.
- Горев В.В., Уваров Б.Ю., Филиппов В.В. и др. Металлические конструкции. В 3т. Т.1. Элементы конструкций: Учеб. для строит. вузов - М., Высш. шк., - 2004. – 551 с.
- Дарков А.В., Шапошников Н.Н. Строительная механика: Учеб. для строит. спец. вузов - М., Высш. шк., - 1986. – 607 с.
- Andreev V.I. The method of optimization of thick-walled shells based on solving inverse problems of the theory of elasticity of inhomogeneous bodies. Computer Aided Optimum Design in Engineering XII. WITpress. 2012. Pp. 189—201.
- V. Andreev, IA Potekhin Modeling equally strong cylinder based iterative approach // International Journal for Computational Civil and Structural Engineering, v. 4, is. 1, 2008, p. 79-84.
- Языев Б.М., Андреев В.И. Выпучивание продольно-сжатых стержней переменной жесткости при ползучести.[Электронный ресурс] // «Инженерный вестник Дона», 2012, №4.– Режим доступа http://www.ivdon.ru/magazine/archive/n4p2y2012/1259 (доступ свободный) – Загл . с экрана. – Яз. рус.
- Литвинов В.В., Языев Б.М. Энергетический метод в форме Тимошенко-Ритца для определения критических сил осевого сжатия круговой цилиндрической оболочки. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1.– Режим доступа http://www.ivdon.ru/magazine/archive/n1y2012/722 (доступ свободный) – Загл . с экрана. – Яз. рус.