Непосредственное векторное управление асинхронными электроприводами с использованием прогнозирующих моделей
Аннотация
Дата поступления статьи: 22.01.2014В статье рассматривается система векторного управления скоростью асинхронного двигателя с непосредственным ориентированием по полю, построенная на основе принципа управления по прогнозирующей модели (МРС). Задача работы – управление скоростью/моментом, потокосцеплением ротора и токами двигателя в системе векторного управления асинхронным двигателем при действии неконтролируемых внешних возмущений со стороны нагрузки. Используются три MPC-регулятора: один - для регулирования скорости вращения двигателя, второй - для управления потокосцеплением ротора, последний предназначен для управления токами двигателя. Простые модели асинхронного двигателя используются в структуре MPC так, чтобы минимизировать вычислительную нагрузку. Представлены результаты цифрового моделирования.
Ключевые слова: Асинхронный электропривод, векторное управление, прогнозирующие модели.
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
В статье рассматривается система векторного управления скоростью асинхронного двигателя, построенная на основе принципа прогнозирующей модели (Model Predictive Control – MPC). Задача данной работы – управление скоростью/моментом, потокосцеплением ротора и токами двигателя в системе векторного управления (ВУ) асинхронным двигателем (АД) с непосредственным ориентированием по полю при действии неконтролируемых внешних возмущений со стороны нагрузки. Используется три MPC-регулятора: один – для регулирования скорости вращения двигателя, второй – для управления потокосцеплением ротора, последний предназначен для управления токами двигателя. Простые модели асинхронного двигателя используются в структуре MPC так, чтобы минимизировать вычислительную нагрузку на контроллер. Представлены результаты цифрового моделирования.
Управление с прогнозированием по модели (УПМ)
Основные преимущества УПМ [1 - 3]:
- Применимость к широкому классу объектов управления, как простых, так и очень сложных, в том числе объекты с большим запаздыванием, неустойчивые и неминимальнофазовые системы;
- Простая реализация для многоканальных (Multi Input – Multi Output, МІМО) систем с многих переменных;
- Возмущения и ограничения на управляющее воздействие и выходные переменные процесса учитываются изначально, на стадии разработке регулятора.
В данной модели УПМ- регулятор отличается от ПИ- регулятора. УПМ- регулятор имеет два входных сигнала: один сигнал задания, а другой сигнал нагрузки или скорости выходного вала АД, как показано на рис 1.а. Схема осуществления прогноза для дискретного объекта иллюстрируется рис. 1.б.
Общая схема УПМ состоит из следующих действий:
- Измерение или оценивание вектора состояния
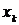реального объекта:
(1)
здесь 
- номер такта, определяющий дискретный момент времени 
, где 
- шаг дискретности. Векторы 
представляют состояние объекта, управление и измерение соответственно в момент времени 
, а
- внешнее возмущение и шум в измерениях в этот же дискретный момент. Матрицы 
имеют постоянные во времени компоненты.
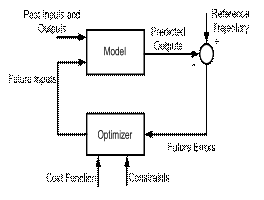
Рис. 1. – а) Базовая структура УПМ- контроллера; б) Схема осуществления прогноза для дискретного объекта.
2. Решение оптимизационной задачи для прогнозирующей модели с начальным условием 
по отношению к:
. (2)
Здесь размерности векторов состояния, управления и измерения такие же, как и в системе (1). Будем полагать, что заданные фиксированные матрицы 
приближенно представляют матрицы 
Пусть прогнозирующая модель (2) на начальном такте 
инициализируется состоянием 
объекта управления, достигнутого на k-м такте его функционирования. Кроме того, пусть выполняются равенства 
для любого 
.
, (3)
где 
и 
- заданные положительно определенные матрицы,
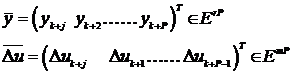(4)
- векторы, представляющие регулируемые и управляющие последовательности соответственно на горизонте прогноза. Использование функционала (3), наряду с оптимизацией динамики, позволяет обеспечить астатизм замкнутой системы.
Ранее рассматривалась оптимизационная задача
(5)
о поиске программной последовательности векторов 
, которая минимизирует функционал (3) c учетом ограничений.
Теперь потребуем, чтобы на любом шаге процесса выполнялись ограничения вида
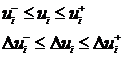(6)
на управляющие переменные и ограничения
(7)
на выходные переменные, где 
- заданные векторы Замечание: неравенства в приведенных уравнениях понимаются по каждой из компонент своих векторов.
- Замена момента времени
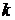на момент 
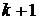и повторение операций, указанных на стадиях 1 - 3.
Заметим, вопрос о минимизации интегрального КФ при наличии ограничений сводится к стандартной задаче численного анализа - к задаче выпуклого КФ. Для поиска точки экстремума, которая является либо внутренней, либо граничной точкой множества, могут быть привлечены известные численные методы. В данной работе используется метод барьерной функции, не требующий большого объема памяти.
Исследование работы УПМ в системе векторного управления асинхронным двигателем
В данной работе для синтеза регуляторов использовались линеаризованные модели АД, как в [4 - 6], не подразумевающие оценивания возмущений и производных типа [7, 8].
Поэтому ее порядок снижен путем применения упрощенной модели механической части электропривода. При векторном управлении моментом операторное уравнение двигателя в составе УПМ- контроллера скорости может быть записано как
. (8)
Упрощенная линеаризованная модель АД описана в составе УПМ- контроллера токов как
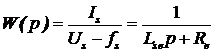, (9)
где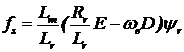 
.
Упрощенная линеаризованная модель АД в составе УПМ- контроллера потокосцепления:
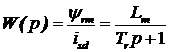. (10)
Результаты моделирования
Построение динамических характеристик системы векторного управления АД будем производить методом цифрового моделирования в программе «MATLAB-Simulink».
Для сравнения рассмотрим переходные процессы системы управления с ПИ регулятором и УПМ - регулятором. Графики переходных процессов с использованием УПМ - регулятора приведены на рис. 2 при работе на номинальной частоте вращения с номинальной двигательной нагрузкой и на рис. 3 – при работе на 0.005 от номинальной частоте вращения с номинальной нагрузкой. Графики переходных процессов с использованием ПИ- регулятора показаны на рис. 4.
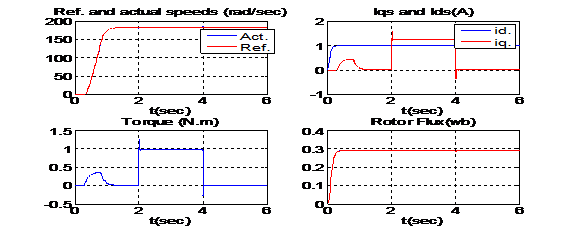
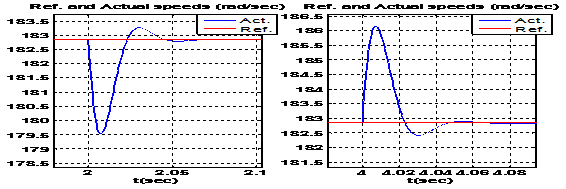
Рис. 2. – Графики переходных процессов в системе ВУ АД с УПМ-регулятором при работе на номинальной частоте вращения с номинальной нагрузкой.
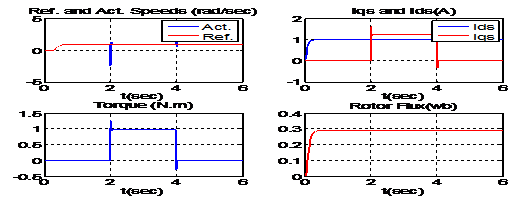
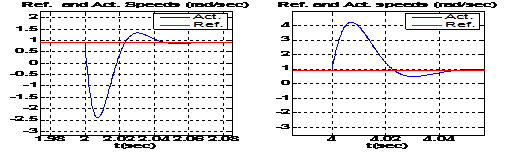
Рис. 3. – Графики переходных процессов в системе ВУ АД с УПМ-регулятором при работе на 0.005 от номинальной частоты вращения с номинальной нагрузкой.
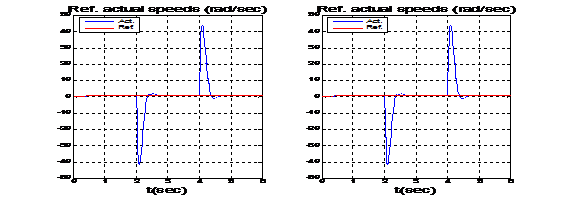
Рис. 4. – Графики переходных процессов в системе ВУ АД с ПИ-регулятором при работе на 0.005 от номинальной частоты вращения с номинальной нагрузкой.
Выводы
С помощью моделирования в программе Matlab-Simulink проведено исследование работы УПМ- регулятора в системах векторного управления скоростью АД. Синтезированная система исследована в статических и динамических режимах. Результаты получены для режимов работы: пуск на холостом ходу и с нагрузкой, внезапный наброс нагрузки в установившемся режиме. Показано, что по величинам тока двигателя, крутящего момента и скорости эффективность УПМ - контроллера оказалась лучше, чем у ПИ- регулятора скорости.
Синтезированная система обеспечивает высокие динамические характеристики, плавность хода и глубокий диапазон регулирования скорости и крутящего момента. Использование в электроприводах отрицательной обратной связи по скорости и УПМ - регуляторов позволяет достигать высокой точности стабилизации заданных скорости и момента, быструю реакцию на внешние возмущающие воздействия при требуемом качестве переходного процесса. Полученные результаты могут быть использованы при построении бездатчиковых систем общепромышленного электропривода [9, 10].
Литература:
1. Коростелев, А.Я. Система с прогнозирующей моделью для управления формой и током плазмы в токамаке [Текст] / Ю.В. Митришкин, А.Я. Коростелев // Проблемы управления. – 2008. – № 5. – С. 19-25.
2. Коростелев, А.Я. Система с прогнозирующей моделью для магнитного управления плазмой в токамаке [Текст] / А.Я. Коростелев, Ю.В. Митришкин // Студенческий научный вестник. Сборник тезисов докладов общеуниверситетской научно-технической конференции Студенческая научная весна - 2007. — М.: НТА АПФН, 2007. — Том IV, часть 1. – С. 183-184.
3. Веремей, Е.И. Пособие «Model Predictive Control Toolbox» [Электронный ресурс] / Е.И. Веремей, В.В. Еремеев, М.В. Сотникова // Режим доступа: http://matlab.exponenta.ru/modelpredict/book1/index.php (доступ свободный) – Загл. с экрана. – Яз. рус.
4. Diab, A.A.Z. Vector controlled induction motor drive based on model predictive control [Текст] / A.A.Z Diab, V.V. Pankratov // Proceedings of ХI International conf. on Actual Problems of Electronic Instrument Engineering APEIE-2012 (Novosibirk, 2 – 4 October 2012 г.), vol. 1. – Novosibirsk: NSTU, 2012. – pp. 167 – 173.
5. Diab, A.Z. Model predictive control of vector controlled induction motor drive [Текст] / A.Z. Diab, V.V. Pankratov // Proceedings of 7th International Forum on Strategic Technology (IFOST). – Tomsk, September 17 – 21, 2012, V. II, pp. 21 – 26.
6. Diab, A.Z. Speed Control of Sensorless Induction Motor Drive Based on Model Predictive Control [Текст] / A.Z. Diab, D.A. Kotin, V.V. Pankratov // Proceedings of 14th International Conference on Young Specialist on Micro/Nanotechnologies and Electron Devices (EDM 2013). – Erlagol, Altai, July 1 – 5, 2013, pp. 269 – 274.
7. Медведев, М.Ю. Оценка возмущений в процессе автоматического регулирования синхронного генератора [Электронный ресурс] / М.Ю. Медведев, В.А. Шевченко // Инженерный вестник Дона, 2013, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/ n4y2013/1930 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Пшихопов, В.Х. Алгоритмическое обеспечение робастных асимптотических наблюдателей производных [Электронный ресурс] / В.Х. Пшихопов, М.Ю. Медведев // Инженерный вестник Дона, 2011, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2011/431 (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Вдовин, В.В. Глобально устойчивый адаптивный наблюдатель для систем общепромышленного асинхронного электропривода [Текст] / В.В. Панкратов, В.В. Вдовин, С.С. Доманов, Г.Г. Ситников // Электротехника. – 2011. – №6. – С.42 – 47.
10. Вдовин, В.В. Синтез адаптивного наблюдателя координат бездатчикового асинхронного электропривода [Текст] / В.В. Вдовин, В.В. Панкратов // Известия Томского политехнического университета. – 2012. – Т. 320, №4. Энергетика. – Томск: Изд-во ТПУ. – С. 147 – 153.