Фрактальный подход при моделировании процессов протекания в капиллярно-пористых средах на примере решения задач обеспечения безопасности жизнедеятельности в чрезвычайных ситуациях и охраны природы

Аннотация

В.В. Янюшкин

Статья посвящена примеру построения математической модели движения броуновских частиц в направлении некоторой твердой поверхности, дается графическая интерпретация полученных результатов. Описана модель осаждения частиц на поверхность переменной длины и приведены количественные характеристики этого процесса. В работе рассмотрены практические вопросы организации и особенности взаимодействия сложных конструкций пылеулавливателей для очистки от различных дисперсных частиц при орошении загрязняющих частиц потоком жидкости. Ключевые слова: пылеулавливатель, пылеподавляющая пластина, воздуховод, воздушный поток, форсунка, распыленная частица

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Южно-Российский государственный технический университет

Введение в проблему.

Возникновение ряда чрезвычайных ситуаций на промышленных объектах приводит к загрязнению окружающей среды с выбросом радиоактивных, химически опасных и биологически опасных веществ. В результате возникают зоны значительного заражения территории, что приводит к невозможности нахождения там людей и животных. В последнее время добавилась новая и трудная задача охраны вод и почвы от загрязнения отходами производства, удобрениями и прочими продуктами жизнедеятельности человечества. В случае ядовитых выбросов важно оценить какова вероятность распространения и масштабы загрязнения. Для построения и моделирования таких явлений широко используются классические подходы физики и геологии, основанные на использовании теорий фильтрации и протекания. Для большинства таких приложений важна пропускная способность пористой среды, то есть характеристика того, насколько легко может протекать в ней жидкость. Особенность таких потоков состоит в том, что вода (или иная рассматриваемая жидкость) движется в капиллярно-пористой среде.
В 1856 г. Дарси установил, что «объем воды, который протекает через слой песка с данными свойствами, пропорционален давлению и обратно пропорционален толщине слоя песка». Многие экспериментальные данные подтверждают справедливость закона Дарси, который лежит в основе большинства современных исследований по теории фильтрации. Но с увеличением скорости создается дополнительный механизм обмена количеством движения; при этом происходит более быстрое возрастание сопротивления с ростом скорости течения и закон Дарси нарушается. К настоящему времени накоплено много данных об отклонении фильтрации от закона Дарси, вместе с тем все гидрогеологические и почвенно-гидрологические расчеты до последнего времени основывались именно на этом законе. Так еще в 1898 г. Кинг опубликовал результаты экспериментов, которые показывают, что закон Дарси нарушается с уменьшением скорости фильтрации. Продолжающееся использование закона Дарси как основы всех фильтрационных расчетов в гидрологии связано с неясностью физической природы наблюдаемых в экспериментах фильтрационных аномалий и путей построения новой теории фильтрации.
Для объяснения наблюдаемых аномалий нарушения закона Дарси обычно привлекались следующие соображения [1]:

• Фильтрующаяся жидкость, содержащая поверхностно-активные компоненты и коллоидные частицы, образует устойчивые коллоидные растворы, которые обладают механической прочностью.
• Механические свойства жидкости постепенно меняются от твердой поверхности к объемной части жидкости: «прочносвязанная» вода — «связанная» вода — «рыхлосвязанная» вода; с увеличением градиента напора в общий поток постепенно вовлекаются слои воды, более прочносвязанные с твердой поверхностью, и эффективная динамическая пористость системы увеличивается.
• Под влиянием поверхности вся вода в порах приобретает свойства неньютоновской жидкости.
• Возникают сопутствующие напорной фильтрации электрокинетические и осмотические эффекты.

В настоящее время наиболее интересен современный подход, основанный на использовании теории фракталов, при этом такие явления можно свести к образованию кластеров или моделированию роста дендритов. Кластер это скопление близко расположенных, тесно связанных друг с другом частиц любой природы. В последнее время термин кластер распространяется и на системы, состоящие из большого числа связанных макроскопических частиц. Введено также понятие фрактального кластера, под которым понимают структуру, образующуюся в результате ассоциации частиц при условии диффузионного характера их движения. Основной чертой фрактального кластера является то, что средняя плотность частиц в нем падает по мере удаления от образующего центра. Таким образом, использование такого подхода в моделировании позволяет максимально приблизить природу движения и распространения вещества в пористой среде.

Основы предлагаемых моделей.

Разработано множество модельных механизмов формирования фрактальных кластеров. Для решения этих задач используется решеточная модель, подробное описание которой представлено в [2-4]. Задание условий протекания вещества в определенном направлении во многом определяет характер получающейся модели.
На рисунке 1 приведен пример результата работы модели при скоплении элементарных частиц и характер их продвижение в некотором изучаемом объекте. Численное моделирование на очень больших решетках показывает, что вероятность образования кластера, протекающего на всю длину решетки, стремится к нулю при размере решетки, стремящейся к бесконечности. Меняя значение порога перколяции, получаются кластеры различных размеров [5]. Это также позволяет моделировать протекание жидкостей с разными значениями текучести и вязкости.
Программно реализуется трехмерная динамическая решеточная модель, в которой можно просмотреть любую вертикальную или горизонтальную проекцию плоскости куба (рис. 2) и проанализировать состояние загрязнения в ней, как показано в таблицах 1-2. На каждой из них показаны наиболее характерные снимки слоев куба, соответствующие состоянию проникновения вещества.
Основная сложность заключается в том, что в реальной пористой среде существует большой разброс пор по размерам и необходимо численно смоделировать процесс протекания, одновременно учитывая поры всех размеров, а также сложно учитывать факторы свойств конкретной жидкости.
Эксперименты с моделью показывают зависимости образования кластеров от порога перколяции и числа этапов существования модели. Число этапов означает применение алгоритмов распространения вещества к уже построенной модели с некоторыми приведенными характеристиками.

Рис. 1. Примеры построения различных перколяционных кластеров

Рис. 2. Схема распространения загрязненных ячеек в трехмерной модели

Таблица 1.
Горизонтальные сечения

Таблица 2.
Вертикальные сечения

При рассмотрении пористой среды как системы с капиллярами одинакового размера в используемых моделях показано, что фронт вещества, движущейся по капиллярам имеет сложную геометрическую конфигурацию.
Поэтому представляют интерес следующие экспериментальные данные и результаты:

• генерация случайных конфигураций кластеров и процесс их развития во времени;
• построение гистограмм распределения для кластеров в различные моменты времени;
• анализ полученных распределений методом Singular Spectrum Analysis (SSA) с целью выявления закономерностей, а также возможностью оперативного прогнозирования и предсказания дальнейшего роста;
• исследование численных характеристик кластеров: получение зависимости числа узлов кластера от модели развития роста; получение зависимости фрактальной размерности кластеров от времени.

Данные проблемы рассмотрены в работе [6], в которой протекание жидкости через пористое тело рассматривается далее как процесс образования кластера на квадратной решетке. Развития кластера можно описать как начальное порождение структуры с последующим переходом ячеек на нижние уровни и увеличением площади, занимаемой загрязненными узлами. Образование множества отростков связано с случайным характером заполнения структуры решетки и распространением жидкости. Получение в конечном итоге единого стягивающего кластера, соединяющего две противоположные стороны квадрата свидетельствует о возникновении эффекта и преодолении порога перколяции и полного протекания через решетку.
Далее строятся гистограммы распределения значений проникновения элементов кластера по структуре решетки. Особенность этих графиков состоит в том, что они показывают динамику изменения роста кластера во времени.
Для дальнейшего анализа характера роста использовался инструмент SSA, который позволяет раскладывать исходные ряды на тренд, колебания (периодики) и шум без задания модели ряда, а затем прогнозировать интерактивно выбранные компоненты на основе порождаемой ими линейной рекуррентной формулы. Данный метод характеризуется простотой и наглядностью в управлении, соединяя в себе достоинства многих других методов, в частности анализа Фурье и регрессионного анализа. Базовый вариант метода состоит в преобразовании одномерного ряда в многомерный с помощью однопараметрической сдвиговой процедуры, в исследовании полученной многомерной траектории с помощью анализа главных компонентов и в восстановлении ряда по выбранным главным компонентам.
Из гистограмм распределения были выделены три основных этапа роста: образование начальных несвязных отростков, интенсивный рост и получение конечного стягивающего кластера. Эти результаты интерпретируются как начальное проникновение, интенсивное протекание в структуре и полное прохождение жидкости через пористое тело. Для каждого из этапов выбрано наиболее вероятное распеределение, которое преобразовано методом SSA. Итоговые результаты опытов приведены на рис. 3-5. 

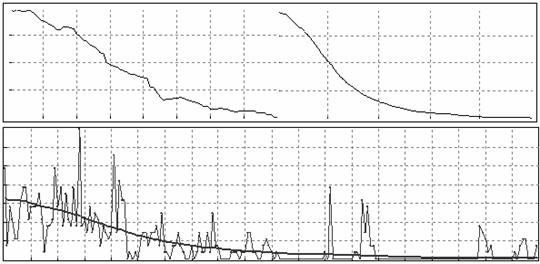
Рис. 3. Этап образования несвязных отростков.

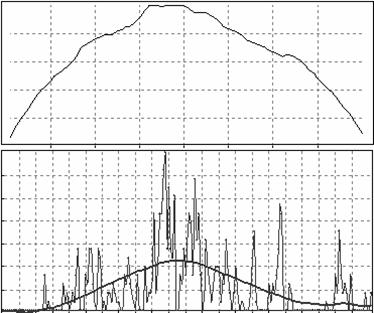
Рис. 4. Этап интенсивного проникновения.

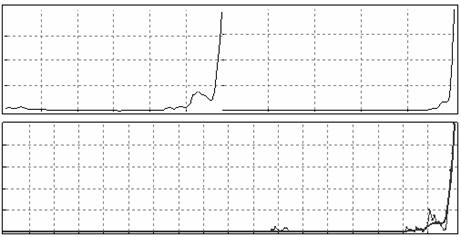
Рис. 5. Этап получения конечного стягивающего кластера.

Как видно из представленных рисунков были получены определенные законы распределения, характерные для случайных процессов. Таким образом, моделирование роста перколяционных кластеров как динамики прохождения жидкости в пористой среде во времени поддается математическому описанию, а значит, может быть проанализировано и с некоторой степенью вероятности предсказан конечный результат. 
Перколяционный кластер, генерируемый на случайной квадратной решетке является примером случайного фрактала. Моделирование роста кластеров с определением их фрактальной размерности предусматривает нахождение такого параметра как центр масс на каждом этапе роста. На рис. 6 показан пример изменения координат центра масс.

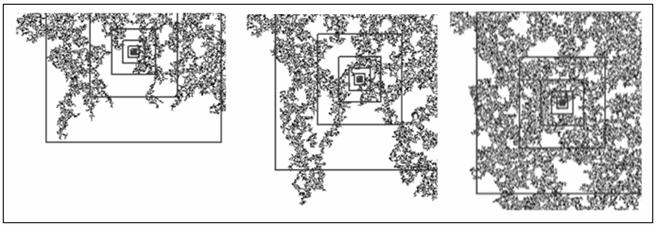
Рис. 6. Изменение центра масс в процессе роста кластера.

Тенденция роста числа узлов кластера, свидетельствует о том, что фактор времени играет важную роль в наполняемости и масштабах распространения загрязнения в пористой структуре. Значительное увеличение площади, занимаемой кластером, показывает высокую интенсивность проникновения рассматриваемой жидкости.
Сложный характер проникновения, а также нерегулярность и изрезанность граничных состояний кластера позволяет отнести подобную структуру к фрактальным поверхностям, для которых размерность никогда не является целочисленным значением. Более того, в приведенных экспериментах показано, что дробная размерность кластера является динамически изменяющимся показателем и может рассматриваться как сложная функциональная зависимость со временем, центром масс кластера и числом заполненных узлов.

Выводы.

Из опыта таких исследований видно, что динамика роста может носить характер, зависящий от многих природных факторов, влияние и вклад каждого из которых учесть достаточно трудно. Но такой подход является во многом оправданным, что позволяет говорить о максимальном приближении к реальности моделируемых явлений и как показывают представленные методики, эффективность применения фракталов для построения моделей загрязнения пористых сред достаточно высока и позволяет адекватно анализировать и оценивать степень и масштабы распространения жидкостей. Классические модели динамики развития аварии обычно показывают сплошной фронт областей заражения, что является не всегда точным и правильным. Взаимодействие загрязняющей жидкости с грунтовыми водами наступает раньше, чем следует из классического анализа. Описанное в статье явление перколяции служит примером случайных (стохастических) фракталов, которые применяются в том случае, когда объект имеет несколько вариантов развития и состояние системы определяется положением, в котором она находится на данный момент. В данных экспериментах фрактальные модели четко указывают на существование различных неоднородностей и лидирующих проникновений заражения, что и является попыткой правильно предугадать хаотичное развитие аварии. На основе данного подхода получено, что при пропитке пористых монодисперсных тел фронт загрязнения имеет экстремальные точки и это необходимо учитывать, например, при подходе фронта к грунтовым водам.
Полученные в результате проведения экспериментов данные на основе созданных программных моделей [7] (зарегистрированных автором в ОФАП) показывают, что фрактальная размерность перколяционных кластеров не является постоянной величиной, а зависит от факторов вероятности заполнения решётки и времени. Дальнейшее значение размерности может приниматься как усредненное значение найденных величин или же, как некоторая функция времени. Доказано, что невозможно предсказать значения переменных хаотической системы, какой является процесс протекания жидкости в пористой среде в определенный момент времени, но можно предсказать качественные особенности поведения этой системы. Умение правильно использовать математические модели и применять их результаты позволит в будущем предотвратить многие негативные последствия техногенных аварий в современном обществе.  

Литература

1. Бондаренко Н.Ф. Физика движения подземных вод. – Ленинград: Гидрометеоиздат, 1973. – 215 с.  
2. Янюшкин В.В. Моделирование процессов загрязнения пористых поверхностей жидкостями на основе фрактальных представлений // «Эврика-2006»: сборник конкурсных работ Всероссийского смотра-конкурса научно-технического творчества студентов высших учебных заведений, г.Новочеркасск, 20-26 ноября 2006 г. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ. – 2006. –  С. 310-312.  
3. Янюшкин В.В. Математическая модель процессов загрязнения пористых поверхностей жидкостями на основе теории фракталов  // «Методы и алгоритмы прикладной математики в технике, медицине и экономике»: материалы VII Международной научно-практической конференции, г.Новочеркасск, 2 февраля 2007 г. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ. – 2007. – Ч.2. – С. 75-77.
4. Власов Ю. В., Фролов А.В., Янюшкин В.В. Моделирование процессов загрязнения пористых поверхностей жидкостями на основе фрактальных представлений // «Безопасность в техносфере». – 2007. – №1. – С. 33-35.           
5. Тарасевич Ю. Ю. Перколяция: теория, приложения, алгоритмы: Учебное пособие. М.: Едиториал УРСС, 2002. – 112 с. 
6. Власов Ю. В., Фролов А.В., Янюшкин В.В. Исследование динамических процессов загрязнения пористых поверхностей и роста перколяционных кластеров // «Безопасность жизнедеятельности». – 2007. – №10. – С. 34-37.
7. Свидетельство об отраслевой регистрации разработки № 6848 «Моделирование процессов загрязнения пористых поверхностей и роста перколяционных кластеров» от 7 сентября 2006 г.

20 июня 2008 г.