Расчет на устойчивость стержней из ЭДТ-10 при различных вариантах закрепления
Аннотация
Статья посвящена исследованию устойчивости полимерных стержней из эпоксидной смолы ЭДТ-10 с учетом начальных несовершенств и развития деформаций ползучести при различных вариантах закрепления стержня.
Ключевые слова: устойчивость стержней, ползучесть, высокоэластические деформации, полимерные материалы, уравнение связи Максвелла-Гуревича.
Полимерные материалы плотно входят в нашу жизнь не только привычными ограждающими, гидроизолирующими материалами, но и имеющими конструкционное предназначение. К ним можно отнести полимерные арматуру, тяжи для крепления навесных потолков и стен. Обладая прекрасными эксплуатационными качествами, такими как кислото- и щелочестойкость, временное сопротивление разрыву некоторых полимеров достигает 2000 МПа, эти материалы не лишены недостатков – для них характерно развитие деформаций ползучести, которая происходит не в фазе в прилагаемой нагрузкой и, соответственно, с напряжениями в теле.
Исследованию устойчивости стержней посвящено много литературы, к примеру, ставшей классикой [3]. Однако при исследовании устойчивости стержней авторы в большинстве случаев отталкиваются от уже ставшей «классической» модели закрепления «шарнир-шарнир». Литературы, в которой рассматриваются другие варианты закрепления с учетом возмущающих факторов, а тем более деформаций ползучести, имеется крайне скудное количество.
В свое время вопрос устойчивости полимерных стержней освящен в работах [1, 2]; из современных работ можно выделить работу [4]. К сожалению, они также рассматривают только вариант закрепления «шарнир-шарнир».
Если рассматривать работу на сжатие полимерной арматуры в кладке, то соединительные элементы в креплении стен нельзя описать только моделью «шарнир-шарнир»; наиболее подходящими будут модели «защемление-защемление» и «защемление-шарнир».
В качестве уравнения связи для таких полимерных конструкций наиболее точно подходит обобщенное нелинейное уравнение Максвелла-Гуревича, в дальнейших расчетах используемое в следующей форме:
где ![]() ;
; 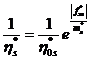 .
.
Здесь ![]() – деформации ползучести,
– деформации ползучести,![]() – модуль высокоэластичности,
– модуль высокоэластичности, ![]() – модуль скорости,
– модуль скорости, ![]() – коэффициент начальной релаксационной вязкости.
– коэффициент начальной релаксационной вязкости.
Для полимерных материалов высокоэластические деформации в общем случае представляют собой суммы отдельных составляющих, каждая из которых соответствует определенному члену спектра времен релаксаций![]() ,
, ![]()
При процессе ползучести до 1000 часов обычно преобладает первая составляющая высокоэластической деформации, так называемый старший спектр времен релаксации, т.е. s=1.
Как видно из выше представленных уравнений определяемые высокоэластические деформации находятся и в левой части уравнения (под оператором дифференцирования), и в правой части (в функции напряжений) ![]() . В связи с этим при использовании уравнения связи Максвелла-Гуревича возникают определенные трудности в применении таких программных комплексов, как ANSYS. Дальнейшее решение задач происходило в программном комплексе MatLab.
. В связи с этим при использовании уравнения связи Максвелла-Гуревича возникают определенные трудности в применении таких программных комплексов, как ANSYS. Дальнейшее решение задач происходило в программном комплексе MatLab.
В практике стержни имеют некоторое искривление своей оси, также называемое «погибью», при этом сила обычно оказывается приложенной внецентренно (см. рис.1.). Подобного рода задачи в упругой постановке, однако, в случае закрепления «шарнир-шарнир», подробно рассмотрены в [1, 3].
Рассмотрим задачу, при которой стержень крепится по схеме «защемление-защемление».
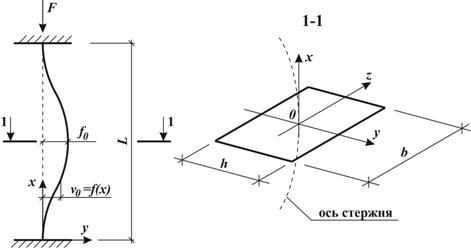
Рис.1. Расчетная схема задачи
При выводе основных уравнений используются следующие допущения и гипотезы:
1. Имеет место одноосное напряженное состояние (![]() ).
).
2. Гипотеза плоских сечений.
3. Геометрическая линейность (![]() , где
, где ![]() – кривизна стержня).
– кривизна стержня).
4. Форма сечения (рассматривается прямоугольное сечение).
Пусть стержень имеет некоторую начальную погибь
где ![]() – начальная стрела прогиба.
– начальная стрела прогиба.
Полную деформацию по оси стержня можно записать в виде
С учетом гипотезы плоских сечений, с другой стороны, можно записать
где ![]() – деформации средней оси стержня.
– деформации средней оси стержня.
С учетом (3) и (4) можно записать
Для любого сечения стержня могут быть записаны интегральные условия
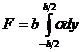 ,
, 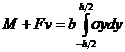 ,(7)
,(7)
где ![]() .
.
Подставляя выражение (5) в (6) и проведя интегрирование, определяются осевые деформации стержня:
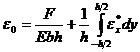 .
. Проводя аналогичные операции с выражениями (5) и (7):
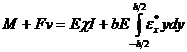 ,
, где ![]() – осевой момент инерции стержня относительно оси z.
– осевой момент инерции стержня относительно оси z.
С учетом того, что ![]() получаем окончательное разрешающее уравнение для оси стержня:
получаем окончательное разрешающее уравнение для оси стержня:
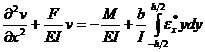 .
. Пусть 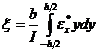 , тогда
, тогда
Граничные условия задачи:
при
Для возможности задания граничных условий применительно к задаче, уравнение (11) дифференцируется дважды по x:
Решение данного уравнения аналитически не представляется возможным даже в случае значительных упрощений, вследствие его структуры решение удобно произвести методом конечных разностей, интегрирование проводится методом Симпсона.
Для варианта закрепления «защемление-шарнир» граничные условия примут вид:
при
Далее рассматриваются задачи ползучести стержня из эпоксидной смолы ЭДТ-10. При этом исходные данные для параметров ползучести взяты из работы [2]. Исходные данные: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для варианта закрепления «защемление-шарнир»: ![]() ,
, ![]() , для варианта закрепления «защемление-защемление»:
, для варианта закрепления «защемление-защемление»: ![]() ,
, ![]() .
.
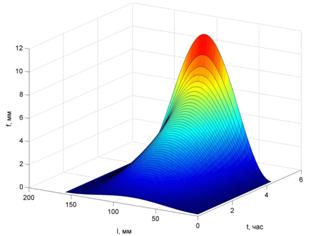
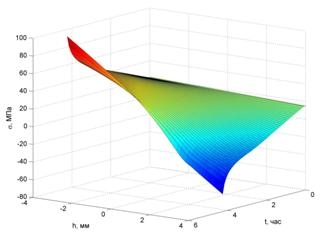
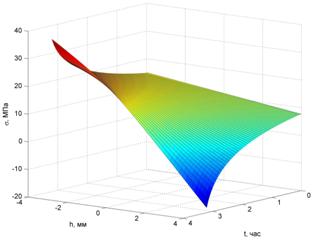
Результаты расчетов представлены на рисунках 2÷5. Положительным напряжениям соответствует сжатие.
Как видно из графиков, в образце при закреплении «защемление-защемление» резко начинают расти деформации при t=4ч15мин, а в образце при закреплении «защемление-шарнир» – при t=3ч05мин.
|
|
|
|
Рис.2. Рост стрелы прогиба во времени в стержне при закреплении «защемление-защемление» |
Рис.3. Рост напряжений в сечении стержня при x=l/2 при закреплении «защемление-защемление» |
|
|
|
|
Рис.4. Рост стрелы прогиба во времени в стержне при закреплении «защемление-шарнир» |
Рис.5. Рост напряжений в сечении стержня при x=l/2 при закреплении «защемление-шарнир» |
Литература:
1. Андреев В.И. Устойчивость полимерных стержней при ползучести: дис. … канд. техн. наук. – М., 1967.
2. Бабич В.Ф. Исследование влияния температуры на механические характеристики полимеров: дис. … канд. техн. наук. – М., 1966.
3. Вольмир А.С. Устойчивость деформируемых систем. – М.: Наука, 1975.
4. Языев С.Б. Устойчивость стержней при ползучести с учетом начальных несовершенств: дис. … канд. техн. наук. – Ростов-н/Д, 2010.