Использование системы остаточных классов для маломощных приложений цифровой обработки сигналов

Аннотация

Н.С. Эрдниева

Дата поступления статьи: 30.04.2013

В статье рассмотрено сравнение энергопотребления дополнительного двоичного кода и системы остаточных классов для приложений цифровой обработки сигналов.

Ключевые слова: система остаточных классов, цифровая обработка сигналов

05.02.02 - Машиноведение, системы приводов и детали машин

05.02.08 - Технология машиностроения

Введение
Решение широкого круга вычислительных задач цифровой обработки сигналов (ЦОС) требует колоссальных объемов математических расчетов. Анализ известных подходов [1] показывает, что при разработке высокоскоростных вычислений требуется применение тех или иных форм параллельной обработки. В последнее время применяют систему остаточных классов (СОК), которая обеспечивает параллелизм на уровне выполнения элементарных операций [2].
Одной из основных проблем цифровой фильтрации является энергопотребление. Известны различные методы для решения проблемы. В работе [3] авторы предложили использовать представление числа СОК как метод снижения энергии в реализации ЦОС архитектуры. Для проверки подхода были разработаны различные эксперименты реализации КИХ-фильтрации, которые представляются с помощью дополнительного двоичного кода (ДДК) и СОК. Эксперименты показали значительное снижение энергии для представления СОК. Целью статьи является объяснение причин снижения энергии.
Основы СОК
Целое представление числа на основе СОК определяется множеством P взаимно простых чисел , называемый основанием СОК. Динамический диапазон основания P - .
Целое  имеет единственное представление СОК:

где  означает .
Если  представляет общие арифметические операции (сложение, разность, произведение, модульное деление), то наиболее интересным свойством СОК [4, 5] является возможность перевода этой операции среди целых чисел в набор модульных операций на различных модулях :
       (1)
Снижение энергопотребления
В цифровой фильтрации [6, 7] возможны различные уровни оптимизации энергопотребления: 1) алгоритмический уровень; 2) архитектурный уровень; 3) арифметический уровень; 4) осуществленный уровень; 5) технологический уровень.
В данной статье рассмотрена оптимизация уровня арифметики с использованием представления СОК. Также проанализирована эффективность ЦОС алгоритмов, реализованных с помощью двух технологий: 1) специализированные интегральные схемы стандартные ячейки (СПИС-СЯ); 2) программируемые логические интегральные схемы (ПЛИС). СПИС-СЯ характеризуются изменчивой логикой и соединительными структурами. ПЛИС имеют фиксированную структуру конфигурируемых логических блоков (КЛБ), тактирования и соединений. Для СПИС-СЯ общая оценка расхода энергии является более сложной.
В данном анализе,  и  представляют собой площадь и энергопотребление фильтра, а х - представление системы счисления, может принимать два значения СОК или ДДК. В общем,  и  растет линейно с числом отводов (), в соответствии с законами 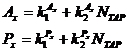(2).
(2)
Константы  представляют смещения графиков площади и энергии, а  являются ростом значения скорости. Пример показан на рис. 1.

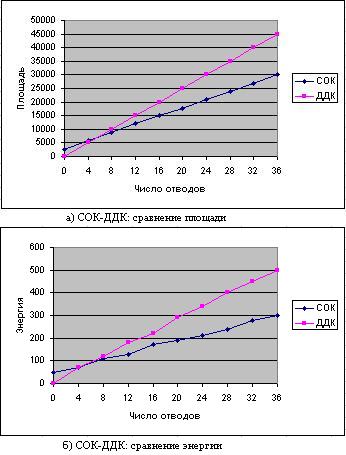
Рис.  1. – Сравнения ДДК и СОК реализаций КИХ-фильтров

Из этих графиков, видно, что СОК имеет большие значения смещения. Это связано с наличием входного и выходного преобразователей. С другой стороны, склоны СОК менее крутые, чем склоны ДДК.
СПИС-СЯ: расходы энергопотребления
Расходы энергопотребления делятся на локальные и глобальные соединения. В то время как сигналы маршрута локальных соединений осуществляются внутри функциональных блоков, сигналы маршрута глобальных соединений - между различными блоками [8].
На рис. 2 изображено распределение по выбранным системам. Рис. 2.а показывает, что локальные соединения играют фундаментальную роль в энергопотреблении. Распределение локального энергопотребления соединений показано на рис. 2.б. Расходы делятся на три группы:

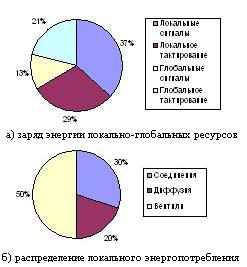
Рис.  2. – СПИС-СЯ расходы энергии

1) энергия для заряда вентилей (50%); 2) энергия для соединений логической емкости заряда (30%); 3) энергия для заряда диффузии логической емкости (20%).
В технологии СПИС-СЯ распространение переноса свойств СОК потенциально дают следующие преимущества площади-энергии: 1) уменьшение сложности (количество вентилей - площади); 2) восстановление соединения логической емкости.
В данной модели выразим площадь СПИС A с точки зрения числа (NAND2) эквивалентных вентилей. Термин  - это число узлов. Логическая емкость  связана в каждом узле i. Учитывая постоянный коэффициент активности переключения , расход энергии выражается
    (3)
Если , F, и  можно считать константами, то получим, суммарная энергия  пропорциональна суммарной логической емкости . Выше изложенные соображения позволяют получить модель для изучения свойств СОК.
Для логической емкости можно получить следующее выражение
      (4)
где  представляет узел логической емкости, полученный сочетанием длины линии  и узла разветвления  с двумя коэффициентами ( и ). Среднее значение этой логической емкости
  (5)
Таким образом, общая логическая емкость
       (6)
где  - число узлов схемы. Из приведенных выражений получим следующие значения энергопотребления
   (7)
Если число вентилей увеличивается, логическая емкость глобальных соединений изменяется по двум причинам: 1) увеличение числа узлов (количество выходов); 2) увеличение длины провода (увеличение сигнала глобальности).
Черновая модель значения логической емкости может предположить: 1)  пропорциональна сложности схем (число вентилей или площади): ; 2)  связаны с сигналом локальности (через Индекс Глобальности или GI)

Следовательно, мы получаем
 с  и наконец,
    (8)
выражает зависимость рассеиваемой энергии по индексу глобальности GI.
Приведем сравнение результатов, полученных для реализации СОК и ДДК КИХ-фильтров на основе технологии СПИС-СЯ. Из выражения (8), получаем коэффициент энергии
       (9)
В эксперименте измеряются соотношения площади () и энергии (). Из этих соотношений можно вывести соотношение GI ():
    (10)
Используя данные из [2] и уравнения (10) получаем соотношения, представленные в Таблице 1. Результаты показывают, что локальность (GI) не играет существенной роли в экономии энергии для СПИС-СЯ реализации (близка к 1), кроме фильтра 3. Для комплексного КИХ-фильтра разница связана с коэффициентом активности, который значительно меньше для Квадратичной СОК (КСОК), как освещено в [9].
Таблица №1
Соотношения площади, энергии и глобальности для СПИС-СЯ

ПЛИС: Расходы энергопотребления
В реализации ПЛИС коэффициенты веса совершенно разные. Анализ энергопотребления ПЛИС выделяет три основных достижения [10]: 1) энергопотребление в логике и элементах ввода-вывода (ЭВВ); 2) энергопотребление в синхронизации структуры; 3) энергопотребление в соединениях. Распределение этих достижений в общей реализации ПЛИС показано на рис. 3, из которого видно, что для данной технологии энергопотребление соединений играет фундаментальную роль.
В технологии ПЛИС предпочтение отдается локальности СОК. Для анализа потребления ПЛИС используется та же модель, что и для СПИС-СЯ. В этом случае площадь соответствует числу долей. Влияние локальности СОК очевидно в Таблице 2. Для технологии ПЛИС отношение GI () составляет около 0,5.

Рис.  3. – Распределение энергопотребления для реализации ПЛИС

Таблица №2
Соотношения площади, энергии и глобальности для ПЛИС

Заключение
В данной статье описано сравнение энергопотребления СОК и ДДК для приложений ЦОС. Анализ проведен на СПИС-СЯ и ПЛИС реализациях. Были проанализированы различные материалы с использованием соотношений площади (A), энергии (P) и глобального индекса (GI). Анализ дал следующие результаты: 1) СОК позволяет снизить энергию как в СПИС-СЯ, так и в ПЛИС реализации; 2) реализация ПЛИС используется как уменьшение сложности и локальности представления СОК. Эти свойства СОК позволят расширить использование технологии ПЛИС к ограничению энергопотребления ЦОС системы.

Литература:

1. Червяков Н.И. Реализация высокоэффективной модулярной цифровой обработки сигналов на основе программируемых логических интегральных схем // Нейрокомпьютеры: разработка, применение, 2006. - №10. – с. 24-35.
2. Бабенко М.Г., Вершкова Н.Н., Кучеров Н.Н., Кучуков В.А. Разработка генератора псевдослучайных чисел на точках эллиптической кривой [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1408 (доступ свободный) – Загл. с экрана. – Яз. рус.
3. Cardarilli G.C., Nannarelli A. and Re M. Residue Nuber System for Low-Power DSP Applications // Proceedings of 2007 IEEE International. Symposium on Circuits and Systems (ISCAS), 2007. – p. 1412-1416.
4. Червяков Н.И. и др. Применение искусственных нейронных сетей и системы остаточных классов в криптографии. – М.: Физматлит, 2012. – 280 с.
5. Червяков Н.И., Сахнюк П.А., Шапошников А.В., Макоха А.Н. Нейрокомпьютеры в системе остаточных классов. Кн. 11: Учебное пособие для вузов. – М.: Радиотехника, 2003. – 272 с.
6. Червяков Н.И. и др. Модулярные параллельные вычислительные структуры нейропроцессорных систем. – М.: Физматлит, 2003. – 288 с.
7. Синельщиков П.В., Чернов А.В. Использование непрерывного вейвлет преобразования для анализа токового сигнала при диагностировании дефектов в червячной передаче [Электронный ресурс] // «Инженерный вестник Дона», 2011, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2011/500 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Magen N., Kolodny A., Weiser U. and Shamir N. Interconnect-power Dissipation in a Microprocessor // Proceedings of SLIP’04, Paris, France, February 2004.
9. Stouraitis T. and Paliouras V. Considering the alternatives in Low-Power Design // in IEEE Circuits and Devices, July 2001.
10. Shang L., Kaviani A.S. and Bathala K. Dynamic Power Consumption in Virtex-II FPGA Family // Proceedings of FPGA’02, Monterey, California, USA. February, 2002.