Исследование напряжений на линии сопряжения ступенчатой пластины

Аннотация

П.В. Дородов

Дата поступления статьи: 15.05.2013

В статье приведено решение задачи о концентрации напряжений возле резкого перехода от одного сечения к другому в элементах конструкций и деталях машин посредством использования одного сингулярного интегрального уравнения. Представлено аналитическое выражение для определения коэффициента концентрации напряжений в зависимости от радиуса кривизны галтели.

Ключевые слова: Ступенчатая пластина, особое интегральное уравнение, линия сопряжения, коэффициент концентрации напряжений

05.02.02 - Машиноведение, системы приводов и детали машин

05.02.08 - Технология машиностроения

Различные детали и рабочие органы машин могут иметь резкие переходы от одного сечения к другому. В этих зонах проявляется значительная концентрация напряжений под действием внешних нагрузок, приводящая к возникновению трещин или больших остаточных деформаций, что является недопустимым явлением. Известно много методов определения напряжений в таких зонах. [1, 2] В данной работе предлагается метод определения напряжений и коэффициента концентрации, позволяющий прийти к точному решению задачи.
На примере плоской задачи рассмотрим сопряжение ступени 1 и основания 2 пластины переменной жесткости (рис.1). Линия сопряжения представляет собой прямую [-t;t], соединяющую углы перехода от ступени к основанию.

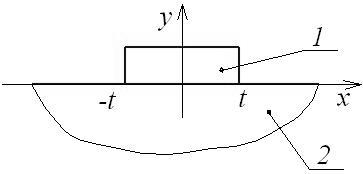
Рис. 1 Сопряжение ступенчатой пластины: 1 – ступень, 2 – основание

Для решения этой задачи используем характеристическую часть особого интегрального уравнения с постоянными коэффициентами а и b на отрезке [-t;t] [3, 4, 5]:
,
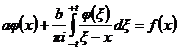где ; U, V – перемещения точек линии сопряжения; ; – нормальные и касательные напряжения на линии сопряжения.
На рисунке 2 изображена пластина после внедрения ступени в основание.

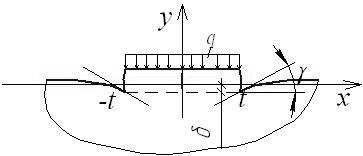
Рис. 2 Ступень после внедрения в основание
q – внешняя нагрузка; δ – вертикальное перемещение линии сопряжения; γ – угол наклона касательной в точке перехода контура пластины от ступени к основанию

В случае неограниченного решения в узлах  имеем [3, 4, 6]:
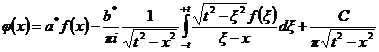,     (1)
где а*, b*, С– постоянные.
Предположим, что линия сопряжения после нагружения пластины остается прямой или ее искривлением можно пренебречь, тогда на линии интегрирования перемещения принимают вид:

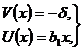
где δ, b <ыги>1 – некоторые постоянные и
,
а выражение (1) после разложения на действительную и мнимую части можно переписать
; .    (2)
Кроме напряжений σ_у и τ_ху возникает еще и σ_х, которое можно определить по закону Гука
,   (3)
где , G – модуль сдвига, ν – коэффициент Пуассона.
Для определения постоянных воспользуемся уравнением равновесия:
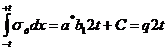          (4)
и краевым условием – при х=0 нормальные напряжения из условий симметрии будут равны главным:

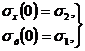
тогда для максимальных касательные напряжений запишем

или с учетом (2) и (3), имеем
.    (5)
Решая совместно (4) и (5), получаем:

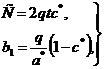
где
, ,
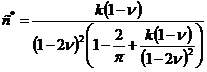а напряжения примут вид:
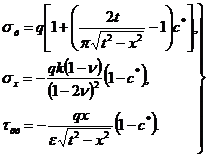       (6)
Из формул (6) видно, что на концах линии сопряжения напряжения σ_у и τ_ху неограниченно возрастают. Это объясняется идеально острыми углами. На самом деле углы скруглены. Переход от ступени к основанию пластины с закругленными углами изображен на рисунке 3.

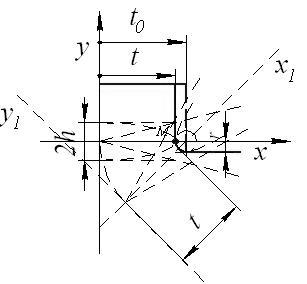
Рис. 3 Ступенчатая пластина со скругленными углами

Обозначим через ασ теоретический коэффициент концентрации напряжений по нормальным напряжениям σ_у, то есть
.
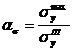Здесь
,
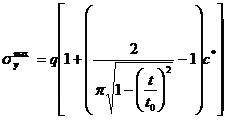где t₀ – полуширина ступени пластины с идеально прямыми (неокругленными) углами,
.
Тогда имеем

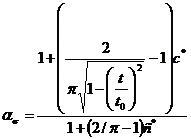
откуда
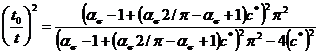.        (7)
Далее предположим, что скругленный угол по контуру совпадает с частью гиперболы (см. рис. 3)

в системе координат х₁, у₁ с действительной t и мнимой h полуосями. Оси х₁, у₁ повернуты к осям х, у под углом в 450.
Тогда для точки М скругленного контура можно записать
.   (8)
Так как α_σ зависит только от геометрии угла, следовательно, в точках линии гиперболы и эллипса с одинаковой кривизной коэффициенты концентрации должны быть одинаковы. Согласно [7, 8] для эллипса имеем:
,
откуда
.  (9)
Учитывая (9), из выражения (8) получаем
.     (10)
Приравнивая правые части (7) и (10), имеем
.
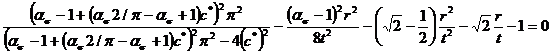Обозначим относительный радиус , тогда последнее выражение можно переписать
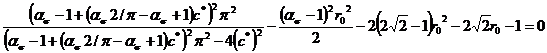.  (11)
На рисунке 4 изображена графическая зависимость (11) теоретического коэффициента концентрации напряжений от радиуса кривизны галтели и коэффициента Пуассона, который для всех материалов принимает значения  и которому соответствует . Построение проводилось в среде пакета программ Maple. Предложенное решение хорошо согласуется с действительным коэффициентом концентрации напряжений, найденным для модели из органического стекла (ν=0,35) при помощи лазерного интерферометра по методике, описанной в [9, 10]. Так, при  действительный коэффициент концентрации составил 1,48, а теоретическое значение, найденное по выражению (11) дает 1,52, то есть относительное отклонение теории от эксперимента равно 2,7%.

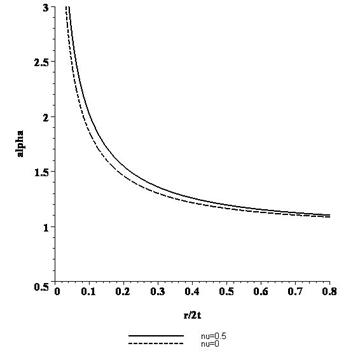
Рис. 4 Графическая взаимосвязь между коэффициентом концентрации напряжений и радиусом галтели

Из анализа графической зависимости можно сделать следующие выводы:
- так как линии с предельными коэффициентами Пуассона практически совпадают, то для исследования концентрации напряжений в галтелях можно пользоваться примерной формулой при
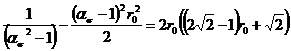;    (12)
- из выражения (12) видно, что  при , а так как в ступенчатых деталях используются выкружки с относительными радиусами  от 0,5 до 0,1, которым соответствуют коэффициенты концентрации напряжений , следовательно, применение технологического скругления углов с постоянными радиусами не является оптимальной формой перехода.

Литература:

1. Попов Г.Я. Концентрация упругих напряжений возле штампов, разрезов, тонких включений и подкреплений. – М.: Наука. Главная редакция физико-математической литературы, 1982. – 344 с.
2. Бескопыльный А.Н. Методика экспериментального исследования предварительных напряжений в образце при вдавливании индентора / А.Н. Бескопыльный, А.А. Веремеенко // Инженерный вестник Дона [Электронный ресурс].– 2012. –№4. – Режим доступа: http://www.ivdon.ru/.
3. Мусхелишвили Н.И. Сингулярные интегральные уравнения. – М.: «Наука», 1968. – 512 с.
4. Дородов П.В. Приведение краевой задачи для плоского упругого тела к одному особому интегральному уравнению / П.В. Дородов // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета (Научный журнал КубГАУ) [Электронный ресурс]. – Краснодар: КубГАУ, 2012. – №06(80).  – Режим доступа: http://ej.kubagro.ru/.
5. Дородов П.В. Исследование напряжений в окрестности плоского горизонтального выреза / П.В. Дородов, А.В. Кулагин // Инженерный вестник Дона [Электронный ресурс].– 2012. –№2. – Режим доступа: http://www.ivdon.ru/.
6. Trjitzinsky W.J. Singular integral equations with Cauchy kernels // Trans. Amer. Math. Soc. 1946. V.60. No. 2. P.167-214.
7. Демидов С.П. Теория упругости: Учебник для вузов. – М.: Высш. школа, 1979. – 432 с.
8. Inglis C.E. Stresses in а plate due to the presence of cracks and sharp corners // Trans. Institute of Naval Architects. 1913. V.55. P. 219-241.
9. Беркутов В.П. Интерферометр для определения нормальных напряжений в плоских прозрачных моделях / Н.В. Гусева, П.В. Дородов, М.М. Киселев // Датчики и системы, – №2. – 2009. – С. 26-30.
10. Беркутов В.П. Полярископ для определения разности главных напряжений в плоских моделях, изготовленных из оптически малочувствительных прозрачных материалов / Н.В. Гусева, П.В. Дородов, М.М. Киселев // Вестник Ижевского государственного технического университета, – №4 (40). – 2008. – С. 108-110.