Упрощенное определение расхождений между минимальными ресурсами выборок и совокупностей для ответственных деталей машин
Аннотация
Дата поступления статьи: 09.06.2013В статье предлагается упрощенный метод расчета гамма – процентного усталостного ресурса стрелы одноковшового экскаватора для совокупности конечного объема, с помощью алгоритма определения упрощенного расхождения между минимальными ресурсами по выборке и совокупности.
Проведенный вычислительный эксперимент показал, что разработанный метод позволяет получить гамма-процентное значение усталостного ресурса стрелы одноковшового экскаватора с помощью перехода от выборочных данных к данным совокупности с расхождениями Ủ=12-31 раза .Ключевые слова: ресурс, стрела, экскаватор, совокупность, Вейбулл
На протяжении многих лет и даже десятилетий исследователи при решении вероятностно-статистических задач использовали выборочный метод определения параметров законов распределения значений тех или иных факторов [1,3,9,10]. Это объяснялось тем, что генеральные совокупности считались бесконечными. Вместе с тем в деятельности человека при ограниченной продолжительности жизни генеральные совокупности являются конечными (автомобили – в миллионах, строительные и сельхозмашины – в тысячах, ракеты – в сотнях и т.д.) При этом выборочный метод актуален, т.к. позволяет существенно снизить затраты на проведение исследований при выборках объемом n=10-100.
Однако существует связь между объемами выборки и генеральной совокупности конечного объема (далее совокупность) (рис. 1).
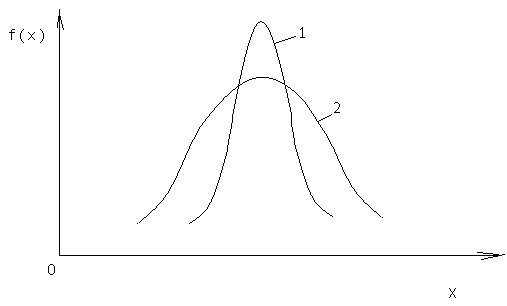
Рис. 1. Плотность распределения:1- выборка; 2- совокупность
Известно, что с увеличением объема выборки возрастает среднее квадратическое отклонение вплоть до равенства его с аналогичным отклонением совокупности.
При использовании для аппроксимации выборочных данных законов со сдвигом, например, законов Вейбулла с тремя параметрами [2] и Фишера-Типпета [10] эти две плотности на рис. 1 примут следующий вид (рис.2).
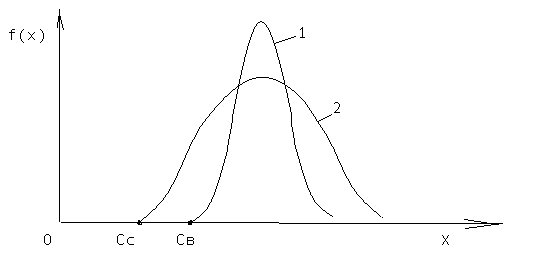
Рис. 2. Плотность распределения трехпараметрического закона Вейбулла: 1 - выборка; 2- совокупность; Сс, Св – сдвиги распределений совокупности и выборки
Параметры Св и Сс обычно находят для определения минимальных значений каких-либо факторов: прочности, ресурса и т.п.
Так, выборочный минимальный ресурс детали, узла, машины будет больше ресурса совокупности. Это означает завышенный выборочный расчетный или экспериментальный ресурс. Для совокупности данный ресурс будет заниженным и, следовательно, характеризоваться преждевременными отказами и материальными затратами [4,5,6,7,8].
Поэтому при наличии выборочных данных было бы очень важно решить задачу более простого перехода от выборочного ресурса к ресурсу совокупности, особенно если совокупность составляет объем Nс=103-105.
Применительно к задаче об определении усталостного ресурса рассматриваются следующая формула
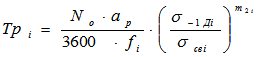 ,
,
где ар – сумма относительных усталостных повреждений;
N0 – базовое число циклов, ц;
f - частота нагружения, Гц;
σ-1 = предел выносливости образцов
Объем выборки n=50; объем совокупности Ne=104.
На рис. 3 представлен алгоритм определения упрощенного расхождения между минимальными ресурсами по выборке и совокупности.
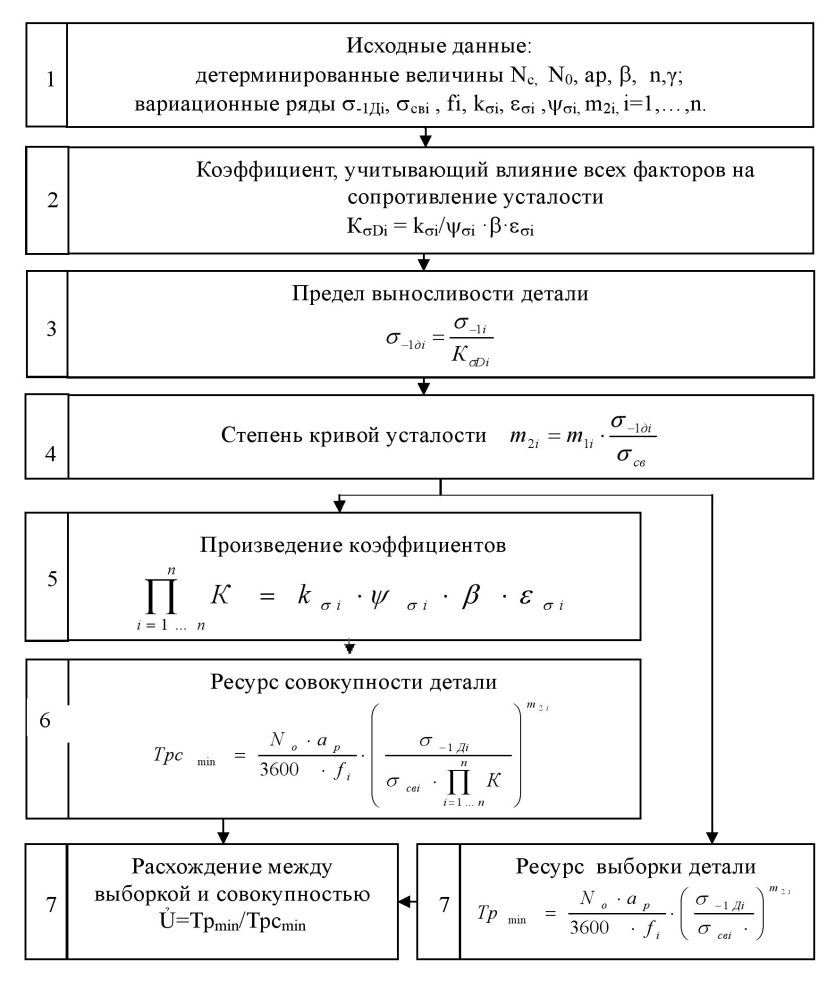
Рис. 3. Алгоритм определения упрощенного расхождения между минимальными ресурсами по выборке и совокупности
В таблице представлены расхождения между ресурсом выборки и ресурсом совокупности выполненные по данному алгоритму
Таблица.
Расхождения между минимальными ресурсами выборки и совокупности
| Стали | Трmin | Трсmin | Ủ |
| Ст 3 10 мм | 19945,31 | 631,592 | 31,579 |
| Ст 3 12 мм | 151010,4 | 5808,728 | 25,997 |
| Ст 3 14 мм | 126265,1 | 5621,087 | 22,462 |
| Ст 3* 10 мм | 141508,8 | 5544,862 | 25,521 |
| Ст 3* 12 мм | 293351,8 | 12681,99 | 23,131 |
| Ст 3* 14 мм | 380652,2 | 13995,71 | 27,197 |
| 09Г2С 8 мм | 251352,5 | 20440,35 | 12,296 |
Таким образом, из таблицы видно, что минимальный ресурс выборки в 12-31 раза больше ресурса совокупности, что объясняет появление ранних отказов деталей совокупности.
Литература
1. Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648с.
2. ГОСТ 11.007-75. Прикладная статистика. Правила определения оценок и доверительных границ для параметров распределения Вейбулла. М.: Изд-во стандартов, 1975. - 30 с.
3. Серенсен С.В., Кагаев В.П., Шнейдерович Р.М. Несущая способность и расчеты деталей машин на прочность. – М.: Машиностроение, 1975. – 488с.
4. Касьянов В.Е., Зайцева М.М., Котесова А.А., Котесов А.А. Оценка параметров распределения Вейбулла для совокупности конечного объема. Деп. ВИНИТИ № 21-В2012 от 24.01.12
5. Котесова А.А., Зайцева М.М., Котесов А.А. Определение действующего напряжения в стреле одноковшового экскаватора [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://ivdon.ru (доступ свободный) – Загл. с экрана. – Яз. рус.
6. Касьянов В.Е., Котесов А.А., Котесова А.А. Аналитическое определение параметров закона Вейбулла для генеральной совокупности конечного объема по выборочным данным прочности стали [Электронный ресурс] // «Инженерный вестник Дона», 2012, №2. – Режим доступа: http://ivdon.ru (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Касьянов В.Е., Зайцева М.М., Котесова А.А., Котесов А.А., Котова С.В. Расчетно-экспериментальное определение гамма-процентного ресурса стрелы одноковшового экскаватора для генеральной совокупности конечного объема [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1 (часть 2). – Режим доступа: http://ivdon.ru (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Касьянов В.Е., Щулькин Л.П., Котесова А.А., Котова С.В / Алгоритм определения параметров прочности, нагруженности и ресурса с помощью аналитического перехода от выборочных данных к данным совокупности [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://ivdon.ru (доступ свободный) – Загл. с экрана. – Яз. рус. 9. Applied statistics and probability for engineers / Douglas C. Montgomery, George C. Runger.—3rd ed.
10. W.J. DeCoursey / Statistics and Probability for Engineering Applications With Microsoft® Excel. – 2003 – 400 р. – Elsevier Science (USA).