Применение метода Галркина при расчете на устойчивость сжатых стержней с учетом ползучести

М. Ю. Козельская; А. С. Чепурненко; С. В. Литвинов

Применение метода Галёркина при расчете на устойчивость сжатых стержней с учетом ползучести

Аннотация

М. Ю. Козельская, А. С. Чепурненко, С. В. Литвинов

Дата поступления статьи: 25.06.2013

Получены разрешающие уравнения для расчета на устойчивость полимерных сжатых стержней с учетом ползучести методом Галеркина. Задача решена для случая шарнирно-опертого стержня, имеющего начальное искривление в плоскости наименьшей жесткости, а также для случая внецентренного приложения силы. Метод Галеркина применен в сочетании с методом конечных элементов, то есть в качестве базисных функций взяты функции формы. Решение выполнено численно, при помощи программного комплекса Matlab. Рассмотрен вариант стержня с постоянной и переменной по длине жесткостью. Показано, что для стержней переменного сечения при той же массе критическое время увеличилось почти в 4.5 раза. Решение для стержней постоянного сечения хорошо согласуется с известными решениями, полученными методом конечных разностей

Ключевые слова: полимерный стержень, ползучесть, метод Галеркина, устойчивость, переменная жесткость

05.23.17 - Строительная механика

Задачи расчета на устойчивость сжатых стержней с учетом физической нелинейности материала рассматриваются в работах [1-10]. Как правило, решение этих задач сводится к линейному неоднородному дифференциальному уравнению второго или четвертого порядка относительно прогиба. В случае шарнирного опирания стержня разрешающее уравнение имеет вид [5]:

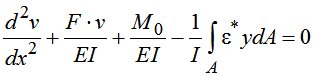. (1)

Решать данное уравнение в работе [5] предлагается методом конечных разностей. Однако этот метод не очень удобен, если стержень имеет переменную по длине геометрию сечения, особенно в том случае, когда жесткость стержня изменяется дискретно.

Рассмотрим решение уравнения (1) методом Галёркина. Сущность этого метода заключается в том, что сначала задаются базисными функциями, которые должны удовлетворять граничным условиям, затем в исходное уравнение подставляют приближенное решение и вычисляют его невязку. Далее выдвигается требование ортогональности невязки к базисным функциям.

Широко используется метод Галёркина в сочетании с методом конечных элементов, то есть когда в качестве базисных функций применяются функции формы.

Для линейного конечного элемента прогиб в произвольной точке выражается через узловые перемещения 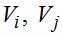в виде:

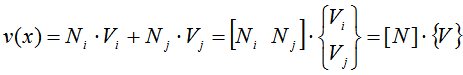, (2)

где .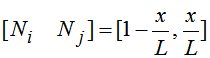

Продифференцировав выражение (2) по x, получим:

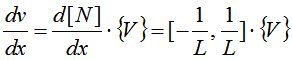Применение метода Галёркина к уравнению (1) приводит к условию:

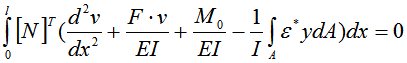. (3)

Интеграл по длине стержня можно разбить на сумму интегралов по длине каждого элемента:

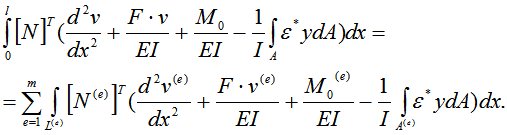(4)

Чтобы понизить порядок производной в интеграле 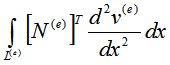, применим интегрирование по частям:

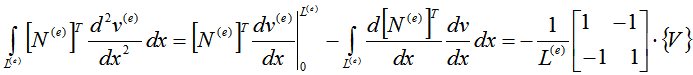Рассмотрим остальные слагаемые, входящие в выражение (4):

;

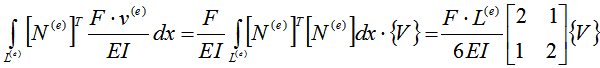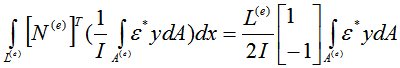В случае, когда сила F приложена с эксцентриситетом e , момент .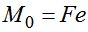

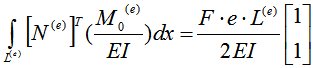Если стержень имеет начальное искривление 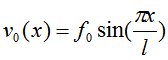, то .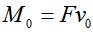

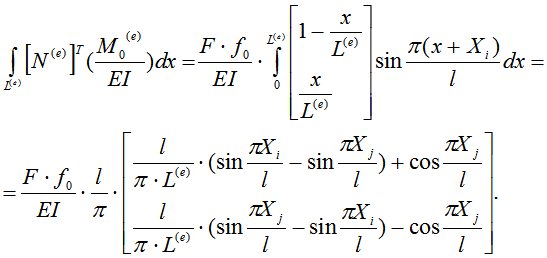
Окончательно условие (3) можно записать в ви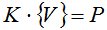де: , где 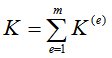– матрица жесткости всего стержня, получаемая суммированием локальных матриц жесткости элементов.

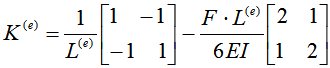Вектор нагрузки:

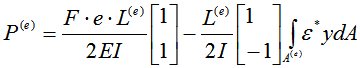– для случая приложения силы с эксцентриситетом.

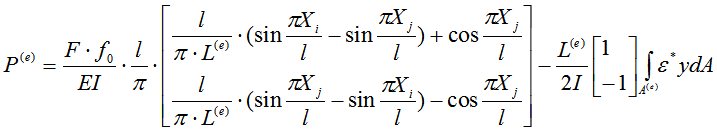– если стержень имеет начальный прогиб.

Для сравнения результатов расчета по методу Галеркина с решениями других авторов будем использовать уравнение связи Максвелла-Гуревича. Данное уравнение применяется в работах[1-5, 7,8]. Оно имеет вид ,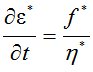

где 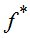- функция напряжений, 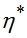- коэффициент релаксационной вязкости.

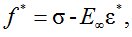
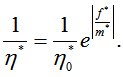
Здесь 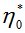– коэффициент начальной релаксационной вязкости; 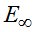– модуль высокоэластичности; 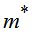– модуль скорости.

Вычисления выполнялись для полимерного стержня прямоугольного сечения размерами b=15мм и h=8мм, материал ЭДТ-10. При расчетах использовались следующие значения: l=157 мм, F=68кг, E=295 кг/мм², E_∞=315 кг/мм², m^*=0.35 кг/мм², η₀=10⁹ кг·с/мм², e=0,16мм. Сравнение результатов расчета с работами И. И. Кулинича [5] и академика В. И. Андреева [4] для случая, когда 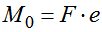, представлено в табл.1.

Таблица №1

Сравнение результатов расчета различных авторов

y, мм	t=54 мин			t=108 мин			t=162 мин
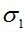y, мм	, МПа	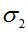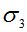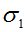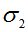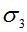, МПа	, МПа	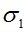, МПа	, МПа	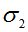, МПа	, МПа	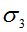, МПа	, МПа
-4	16,000	16,002	15,984	19,310	19,800	19,292	34,435	31,632	32,612
-2	11,152	11,147	11,143	13,305	13,586	13,293	22,893	21,134	21,733
0	5,780	5,780	5,780	5,982	6,010	5,982	6,692	6,680	6,672
2	0,270	0,274	0,278	-1,947	-2,001	-1,733	-9,396	-9,189	-9,906
4	-5,254	-5,247	-5,237	-9,860	-10,00	-9,436	-23,88	-23,80	-24,97

где – результат, полученный И. И. Кулиничем; – результат, полученный академиком РААСН, проф. В. И. Андреевым; – результат, полученный авторами. За 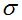здесь обозначены напряжения в середине пролета.

Для сравнения был проведен расчет ступенчатого стержня той же массы, состоящего из 5 участков. График изменения ширины сечения b показан на рис. 1.

На рис. 2 и 3 показаны соответственно графики роста стрелы прогиба для стержней постоянного и переменного сечения. Как видно из графиков,

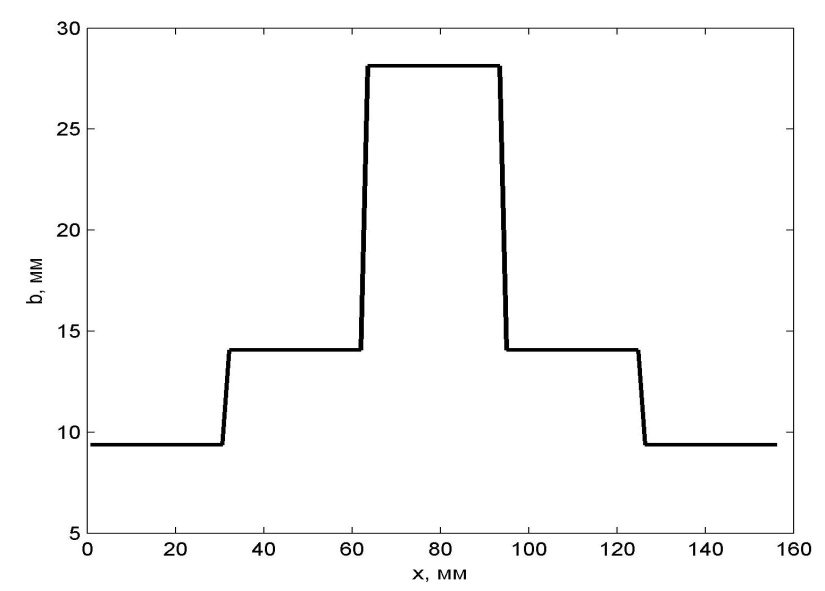
Рис.1. - График изменения ширины сечения b

критическое время для стержней переменной жесткости при той же массе больше почти в 4.5 раза, что свидетельствует об экономической эффективности их применения.

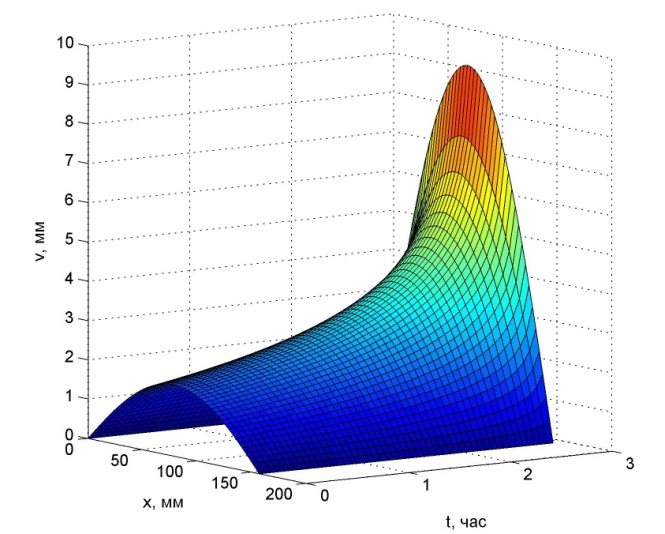Рис. 2.- График изменения стрелы прогиба для стержня постоянного сечения

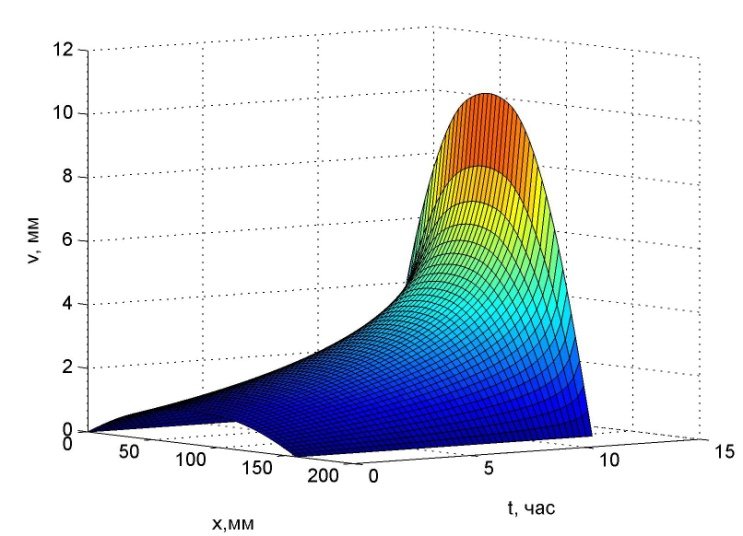Рис. 3. - График изменения стрелы прогиба для стержня переменного сечения

Литература

Литвинов С.В., Клименко Е.С., Кулинич И.И., Языева С.Б., Торлина Е.А. Расчет на устойчивость стержней из ЭДТ-10 при различных вариантах закрепления [Электронный ресурс] // «Инженерный вестник Дона», 2011, №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2011/415 (доступ свободный) – Загл. с экрана. – Яз. рус.
Литвинов С.В., Клименко Е.С., Кулинич И.И., Языева С.Б. Расчет на устойчивость полимерных стержней с учетом деформаций ползучести и начальных несовершенств [Электронный ресурс] // «Инженерный вестник Дона», 2011, №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2011/418 (доступ свободный) – Загл. с экрана. – Яз. рус.
Литвинов С.В., Языев Б.М., Бескопыльный А.Н., Ананьев И.В. Расчет на устойчивость стержней из ЭДТ-10 при начальной погиби стержня в виде S-образной кривой [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2012/723 (доступ свободный) – Загл. с экрана. – Яз. рус.
Андреев В.И. Устойчивость полимерных стержней при ползучести: дис. канд. техн. наук. – М., 1967.
Кулинич И.И. Устойчивость продольно-сжатых стержней переменной жесткости при ползучести: дис. канд. техн. наук. – Ростов-на-Дону, 2012.
Вольмир А.С. Устойчивость деформируемых систем. – М.: Наука, 1975.
Языев С.Б. Устойчивость стержней при ползучести с учетом начальных несовершенств: дис. канд. техн. наук. – Ростов-н/Д, 2010.
Языев Б.М., Андреев В.И. Выпучивание продольно-сжатых стержней переменной жесткости при ползучести.[Электронный ресурс] // «Инженерный вестник Дона», 2012, №4.– Режим доступа http://www.ivdon.ru/magazine/archive/n4p2y2012/1259 (доступ свободный) – Загл . с экрана. – Яз. рус.
Egorov Y.V. On the Lagrange problem about the strongest colonn // Rapport Interne 02-16. Universite Paul Sabatier, Toulouse. 2002. — С. 1-7.
Bleich H.H. Nonlinear creep deformations of columns of rechtangular cross section // Iourn. of Appl. Mech. Dec. 1959