Применение корреляционных функций для оценки погрешности формы деталей машин в поперечном сечении

Аннотация

А.К. Остапчук, В.Е. Овсянников, Е.Ю. Рогов

Дата поступления статьи: 07.05.2014

Рассматриваются вопросы применения аппарата корреляционного анализа для оценки погрешности формы деталей машин в поперечном сечении. Показано, что использование рассматриваемого аппарата также эффективно как и применение традиционных методов оценки погрешности формы, однако требует меньших вычислительных затрат

Ключевые слова: погрешность, форма, детали, корреляция, анализ

Оценка погрешности формы деталей машин в поперечном сечении достаточно сложная задача, ввиду того, что на результат оказывают влияние погрешности установки и смещение измеряемой поверхности (эксцентриситет). Одним из эффективных путей исключения данных погрешностей является использование аппарата Фурье-анализа, который позволяет, исключая соотвествующие гармоники, оценить параметры погрешности формы в поперечном сечении без указанных выше погрешностей [1, 2]. Однако процесс вычислений в данном случае достаточно трудоемкий и сложный, следовательно, Фурье-анализ для оценки параметров погрешности формы будет затруднительно применять в случае оперативной диагностики погрешности формы при обработке на станке.
Таким образом, целью работы является разработка метода оценки погрешности формы деталей машин в поперечном сечении, требующего меньших вычислительных затрат чем метод, основанный на Фурье-анализе, но обладающего такой же информативностью и точностью.  
Одним из перспективных решений является применение корреляционного анализа. Подтверждением этого является эффективность использования корреляционных функций при описании профиля шероховатости [2, 3]. В данном случае профиль детали в поперечном сечении можно описать следующим выражением [3]:
,  (1)                                
Корреляционная функция профиля должна быть представлена системой параметров, установленных ГОСТ 24642-81.
Для расчета корреляционной функции профиля необходимо через параметр отклонения от круглости Fa  выразить следующие величины:
-дисперсию случайной составляющей  равную значению корреляционной функции при .
-коэффициент затухания корреляционной функции случайной компоненты ;
-амплитуду систематической составляющей А;
-шаг систематической составляющей .
Геометрическая интерпретация корреляционной функции приведена на рис. 1:

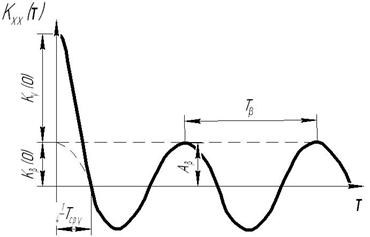
Рис. 1. Геометрическая интерпретация корреляционной функции

Для расчета корреляционной функции профиля поверхности необходимо через параметр поверхности отклонение от круглости Fa  выразить следующие величины:
-дисперсию случайной составляющей равную значению корреляционной функции при .
-коэффициент затухания корреляционной функции случайной компоненты ;
-амплитуду систематической составляющей А;
-шаг систематической составляющей .
При токарной обработке на профиль в поперечном сечении доминирует случайная составляющая. Корреляционная функция этой составляющей с достаточной точностью аппроксимируется выражением
 (2)                                               
При τ=0 имеем:
  (3)                                    
В конечном виде корреляционная функция профиля имеет вид:
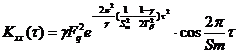,   (4)                                
где T_B – шаг случайной составляющей, Sm – шаг систематической составляющей.
Для экспериментального подтверждения производилось определение корреляционной функции по данным измерений на реальных деталях [4 - 6]. В данном случае значения искомой функции определяются следующим образом:
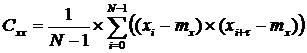,   (5)                                                                                                               
где  - среднее значение величины;  - дисперсия величины.
В качестве данных для анализа использовались измеренные профили реальных деталей, полученные в результате обработки точением: скорость резания V от 100м/мин до 300м/мин, подача S от 0,01мм/об до 0,21мм/об, глубина резания t от 0,25мм до 1,5мм.
В качестве режущего инструмента использовались стандартные токарные резцы с механическим креплением режущих пластин из наиболее распространенных в производстве твердых сплавов Т15К6, ВК8, ВОК60.
Для измерения и анализа виброакустических колебаний включает приборы и регистрирующую аппаратуру приемный преобразователь, усилитель, блок фильтров, комплекс анализа виброасигналов ZetLab (ЗАО «Электронные технологии и метрологические системы»).

Рис. 2. Стенд

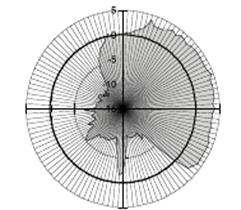
Рис. 3. Отклонение от реального размера n=1000 об/мин; S=40мм/об
Вычисление значений функции (5) производилось в специально разработанной компьютерной программе, см. рис. 4 [7].

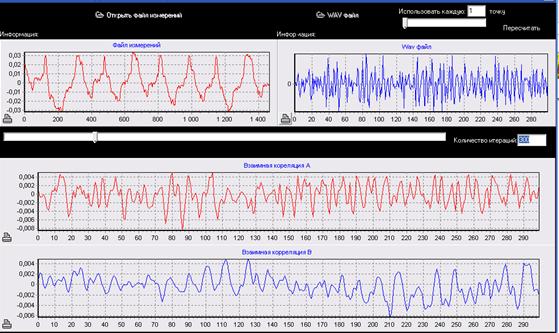
Рис. 4. Интерфейс программы

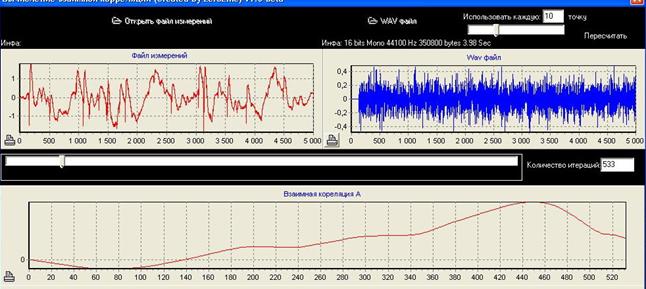
Рис. 5 Результат расчетов взаимной корреляции

Суждение о применимости рассматриваемого аппарата производилось посредством определения взаимной корреляции между оценками погрешности формы посредством Фурье анализа [1, 2, 8, 9, 10] и описания, полученного с использованием выражений (4, 5), которые вычислялись на основе экспериментальных данных. Расчеты показали, что коэффициент взаимной корреляции достигает 0.8 (см. рис. 5), что говорит о сильной взаимосвязи и подтверждает правильность высказанных предположений.

Литература:

1. Остапчук А.К. Метод оценки погрешности  формы деталей гидравлических систем транспортных машин [текст] / А.К. Остапчук, В.Е. Овсянников, Е.Ю. Рогов // Транспорт Урала, №2, 2011. - с. 38-41.
2.  Остапчук А.К. Применение теории случайных процессов для моделирования параметров качества поверхности [текст] / А.К. Остапчук, В.Е. Овсянников, Е.Ю. Рогов // Транспорт Урала, №2, 2011. - с. 41-46.
3. Остапчук А.К. Научные основы обеспечения шероховатости поверхности на базе анализа случайных процессов: Монография [текст] /А.К. Остапчук, В.Е. Овсянников. – Курган: Изд-во Курганского гос. ун-та,2012.- 188 с.
4. Зырянов В.В. Методы оценки адекватности результатов моделирования [электронный ресурс] / В.В. Зырянов // «Инженерный вестник Дона», 2013, №2 − Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2013/1707 (доступ свободный) − Загл. с экрана. – Яз. рус.
5. Квочкин А.И. Параметрический метод измерения разности фаз квазигармоничиских сигналов [электронный ресурс] / А.И. Квочкин, А.В. Никитин, В.К. Игнатьев // «Инженерный вестник Дона», 2013, №3 − Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/1749 (доступ свободный) − Загл. с экрана. – Яз. рус.
6. Овсянников В.Е. Инновации при выглаживании с жестким закреплением индентора: монография [текст] / В.Е. Овсянников, В.Ф. Губанов, В.В. Марфицын. – Lambert academic publishing, Germany, Saabrucken, 2012. – 224 c.
7. «Вычисление взаимной корреляции v1.0»: свидетельство об отраслевой регистрации разработки №10387 / А.К. Остапчук, В.Е. Овсянников, Е.Ю. Рогов. - № 50200800796; заявл. 11.04.2008; опубл. 11.04.2008; Инновации в науке и образовании №4(39). с. 12
8. Bertsekas D.P., Shreve S.E. Stochastic Optimal Control. The Discrete-Time Case. – Athena Scientific, Belmont, Massachusetts, 2006. 330 p.
9. Bertsekas D.P., Shreve S.E. Athena Scientific; 1 edition (February 1, 2007). - 330 p.
10. Stidham S. A. Discounted Analog and a New Proof // Operation Research. - 1972. -Vol. 29. - P. 1115-1126.