Математическое моделирование резонансного туннелирования в полупроводниковых наноструктурах
Аннотация
В работе рассмотрены результаты математического моделирования резонансного туннелирования в полупроводниковых наноструктурах. Разработанная модель позволяет вычислять коэффициенты прохождения через двухбарьерную структуру и отражения от неё носителей заряда в зависимости от их энергии.
Ключевые слова: туннелирование, полупроводниковые наноструктуры, физическая модель, двухбарьерную структуру, уравнение Шредингера, коэффициенты прохождения, математическая модель, алгоритм решения. № гос. регистрации 0420900096/0029
Таганрогский научно–исследовательский институт связи
Эффект резонансного туннелирования в тонкопленочных гетероструктурах является основой создания резонансно-туннельных диодов [1]. Интерес к двухбарьерным квантовым структурам обусловлен видом их N-образной вольт-амперной характеристики с участком отрицательного дифференциального сопротивления и малой инерционностью процесса туннелирования (порядка 10-13 сек).
Эти свойства резонансно-туннельных диодов делают их перспективными для создания высокоскоростных приборов терагерцового диапазона и цифровых устройств с временем переключения порядка 10-12 сек и менее.
В данной работе рассмотрены результаты математического моделирования резонансного туннелирования в полупроводниковых наноструктурах.
Разработанная модель позволяет вычислять коэффициенты прохождения через двухбарьерную структуру и отражения от неё носителей заряда в зависимости от их энергии.
Физическая модель
Пусть двухбарьерная структура расположена на расстояниях от 0 до L, тогда волновая функция описывается уравнением Шредингера:
(1)
Здесь m – эффективная масса электрона, которая считается одинаковой во всей рассматриваемой области. Решением уравнения во внешних областях будут функции вида:
(2)
,
где r и t – амплитуды отражения и прохождения соответственно.
Коэффициенты отражения R и прохождения T есть:
, 
(3)
Граничные условия получим из функций (2):
(4)
Выражая r и tчерез
и 
, граничные условия можно записать:
(5)
Вместе с уравнением (1) условия (5) определяют задачу во внутренней области от 0 до L. Решая эту задачу и найдя 
, мы можем найти коэффициенты отражения и прохождения как:
, 
(6)
Математическая модель
Примем полную длину структуры Lза единицу, тогда уравнение Шредингера примет вид:
(7)
где энергия 
и потенциал 
отсчитываются в единицах 
.
Разобьем участок от 0 до Lна Nобластей L = Na. Тогда, если L=1, то а=1/N.
Для произвольной точки внутри области уравнение (7) можно записать в дискретном виде:
(8)
(9)
Для первого граничного условия (5) сделаем замену производной волновой функции на ее дискретный аналог 
. Тогда граничное условие и уравнение Шредингера при x=n=0 имеют вид:
(10)
Складывая уравнения (10) и разделив на 2, получим первое граничное условие:
(11)
Для второго граничного условия аналогично найдем:
(12)
Откуда получим второе граничное условие в виде:
(13)
Таким образом, задача состоит в решении системы уравнений (8), (11), (13).
Алгоритм решения
Трехдиагональную систему уравнений (8) будем решать модифицированным методом прогонки [2]. Пусть 
, Rn- множитель, зависящий от n. Из уравнения (8) найдем 
, то есть: 
Но, по определению множителя Rn:
(14)
отсюда:
(15)
Из граничного условия (13): 
откуда получаем:
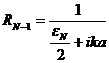(16)
Формулы (15) и (16) позволяют вычислить множители Rn от RN-1 до R0.
Из граничного условия (11) 
, то есть:
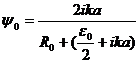(17)
Формулы (17) и (14) позволяют затем найти все значения волновой функции. Амплитуды отражения и прохождения:
, 
. Коэффициенты прохождения и отражения можно найти как:
,
.
Из приведенного ниже графика видно, что коэффициент прохождения носителя заряда через двухбарьерную наноструктуру возрастает, когда значение энергии носителя заряда совпадает с квантованными значениями энергии в этой структуре. Этими значениями можно управлять, создавая структуры с различной геометрией (толщиной слоев полупроводниковых материалов).
Перспективным направлением является разработка приборов с третьим – управляющим шириной барьера электродом, то есть резонансно-туннельным транзистором.
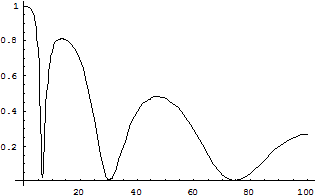
Зависимость коэффициента прохождения от энергии
Список литературы
1. Демиховский В.Я., Вугальтер Г.А. Физика квантовых низкоразмерных структур. М., «Логос», 2000.
2. Ц.На Вычислительные методы решения прикладных граничных задач. М., «Мир», 1982.