Модель поведения автономного сценария в задачах управления распределенными информационными ресурсами
Аннотация
Дата поступления статьи: 27.07.2013В статье получило свое дальнейшее развитие применение технологии автономных сценариев для управления информационными ресурсами вычислительных систем. Формализовано поведение детерминированных и стохастических автономных сценариев с использованием аппарата конечных автоматов, что позволяет разрабатывать модели и технологию решения широкого класса задач управления информационными ресурсами.
Ключевые слова: автономные сценарии, теория конечных автоматов, концепция фреймов, слот, управление распределенными информационными ресурсами.
Введение
Важную роль в повышении эффективности функционирования любого предприятия, интенсификации и развитии управленческих и инновационных процессов играет качество управления информационными ресурсами (УИР), под которыми будем понимать информацию и инструменты работы с нею.
В условиях постоянного развития информационных систем и технологий становится невозможно эффективно решать вручную множество сложных задач управления информационными ресурсами. Поэтому, учитывая все возрастающий спрос на программные средства, которые облегчают администрирование в распределенных системах и выполняют те или иные задачи информационной поддержки, разработчики предлагают все новые решения для управления информационными ресурсами, расширяют возможности существующих программных продуктов.
Однако в настоящее время не существует универсального класса систем УИР, которые отвечали бы потребностям предприятий различных масштабов и разного уровня автоматизации процессов управления. Поэтому поиск доступных, гибких и универсальных средств управления всем многообразием информационных ресурсов распределенных систем является одной из важнейших задач ИТ-индустрии.
Такие свойства программных сценариев, как автономность, целенаправленность, мобильность и адаптивность, а также независимость от сред и квалификации разработчика, способность решать и простые, и сложные задачи, как на сервере, так и на стороне клиента, позволяют рассматривать их как одно из перспективных направлений развития УИР.
Для системной проработки вопросов возможности и целесообразности применения автономных сценариев в автоматизации процессов УИР необходимы формализация и исследование их структуры и поведения при решении различных классов задач УИР.
1Разработка концептуальной модели автономного сценария
Рассмотрим один из подходов к созданию модели универсального автономного сценария, ориентированного на решение задач управления информационными ресурсами вычислительных систем, на основе концепции фреймов [1,2]. В общем случае она может быть записана в виде:
![]() , (1)
, (1)
где FR – имя фрейма;
совокупность <Ri,Сi1,…,Cij,…,Cim> – описание i-го слота фрейма;
Ri – имя i-го слота, Cij – j-ое значение i-го слота.
На основании фрейма (1), может быть реализована модель программного сценария в терминах <объекты>, <условия>, <действия>, <результаты>. Фрейм выступает в виде универсального каркаса или типовой оболочки, в которую могут добавляться функциональные модули-слоты для решения конкретных задач управления информационными ресурсами.
Каждый слот фрейма связан с конкретным объектом информационного пространства и выполняет с ним заданное действие. Математическое описание слота имеет вид:
![]() , (2)
, (2)
где![]() – множество имен атрибутов,
– множество имен атрибутов, ![]() – множество доменов,
– множество доменов, ![]() – отображение
– отображение ![]() ,
, ![]() – множество, определяющее начальные условия и признаки выполнения действий в структуре задания,
– множество, определяющее начальные условия и признаки выполнения действий в структуре задания, ![]() – множество операций, при этом
– множество операций, при этом ![]() , где
, где ![]() – операции над слотами-кортежами,
– операции над слотами-кортежами, ![]() – операции над состояниями кортежей,
– операции над состояниями кортежей, ![]() – операции над значениями типовых атрибутов. При этом
– операции над значениями типовых атрибутов. При этом ![]() , где
, где ![]() – операции над данными одного типа,
– операции над данными одного типа, ![]() – межтиповые операции,
– межтиповые операции, ![]() – модель-кортеж i-го задания автономного сценария.
– модель-кортеж i-го задания автономного сценария.
Кортеж ![]() в модели (2) может быть представлен в виде:
в модели (2) может быть представлен в виде:
![]() , (3)
, (3)
где ![]() – множество состояний кортежа
– множество состояний кортежа ![]() ,
, ![]() – множество ограничений целостности,
– множество ограничений целостности, ![]() – множество операций, заданных на
– множество операций, заданных на ![]() .
.
С учетом (2) и (3) логическую модель автономного сценария можно рассматривать как двумерный объект, имеющий реляционную структуру, слоты-кортежи которой описаны с помощью типового набора атрибутов ![]() [3,4]:
[3,4]:
![]() (4)
(4)
Где в качестве базовых представлены следующие типы:
OBG (object-объект)={база данных, файл, папка, сценарий, том, диск};
ACT(action-действие)={записать, копировать, читать, удалить, искать, наблюдать, защищать, ссылаться, выполнять};
CON(condition-условие)={ЕСЛИ <условие> ТО <предикат> };
FLAG(признак выполнения задания)={0; 1}.
Слот также может иметь ключевой атрибут – идентификатор ID (index-индекс) и атрибут PRI (priority – приоритет), значение которого определяется пользователем и используется для взаимодействия сценариев.
Модель слота автономного сценария показана на рис.1.
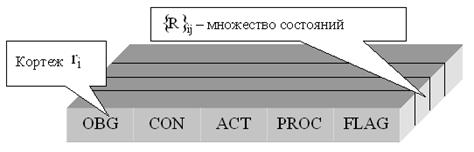
Рис.1. - Модель слота автономного сценария
Состояния-кортежи ![]() могут быть представлены, например, в виде реляционной таблицы, атрибутами которой являются
могут быть представлены, например, в виде реляционной таблицы, атрибутами которой являются ![]() .
.
2 Классификация автономных сценариев на основе фреймовой структуры
Так как во многих реальных ситуациях автономные сценарии должны решать возложенные на них задачи в условиях априорной неопределенности, то достижение ими заданной цели возможно лишь на основе применения адаптивного подхода. Суть такого подхода состоит в использовании текущей информации, получаемой в результате выбора конкретных действий, для обоснования выполнения последующих действий. В задачах адаптивного выбора вариантов такой текущей информацией являются значения потерь, получаемые в результате выбора конкретных вариантов. Это позволяет компенсировать недостаток информации и реализовать оптимальную на классе систем стратегию управления [5].
Рассмотрим общую постановку задачи адаптивного выбора вариантов, представленную на рисунке 2.
Смысл подхода состоит в следующем - в каждый из последовательных моментов времени ![]() необходимо выбирать вариант
необходимо выбирать вариант ![]() из конечного множества возможных вариантов
из конечного множества возможных вариантов ![]() .
.
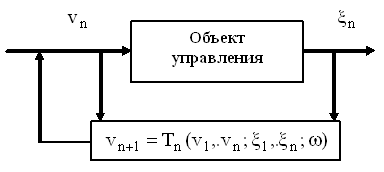
Рис.2. - Схема адаптивного выбора вариантов
Потери системы ![]() представляют собой функцию элементарного исхода
представляют собой функцию элементарного исхода ![]() (имеет бинарные значения «штраф» и «отсутствие штрафа») и зависят от выбранного варианта
(имеет бинарные значения «штраф» и «отсутствие штрафа») и зависят от выбранного варианта ![]() ,а также, возможно, от состояния системы. Реализуемая при этом последовательность вариантов
,а также, возможно, от состояния системы. Реализуемая при этом последовательность вариантов ![]() должна быть такой, чтобы достигалась заданная цель, формулируемая в терминах предельных значений текущих средних потерь.
должна быть такой, чтобы достигалась заданная цель, формулируемая в терминах предельных значений текущих средних потерь.
Выбор очередного варианта ![]() производится на основе полученной к данному моменту времени совокупности потерь
производится на основе полученной к данному моменту времени совокупности потерь ![]() , которая соответствует реализованной последовательности вариантов
, которая соответствует реализованной последовательности вариантов ![]() . Это означает, что
. Это означает, что ![]() является функцией от
является функцией от ![]() ,
, ![]() и, возможно, от момента времени
и, возможно, от момента времени ![]() и элементарного исхода
и элементарного исхода ![]() . Эту функцию
. Эту функцию ![]() назовем правилом выбора варианта
назовем правилом выбора варианта ![]() :
:
![]() ,
, ![]() , (5)
, (5)
где ![]() в зависимости от задачи – либо скаляр, либо вектор.
в зависимости от задачи – либо скаляр, либо вектор.
Функция ![]() может быть как детерминированной, так и случайной (рандомизированной). Последовательность
может быть как детерминированной, так и случайной (рандомизированной). Последовательность ![]() правил выбора определяет стратегию выбора вариантов или стратегию управления информационным пространством [6,7].
правил выбора определяет стратегию выбора вариантов или стратегию управления информационным пространством [6,7].
Неопределенность исхода приводит к необходимости использовать более сложные рандомизированные стратегии. Большинство из них реализуют рандомизированные правила выбора следующего вида:
![]() ,
, ![]() , (6)
, (6)
где ![]() -вектор-функция,
-вектор-функция,
![]() - вектор условных вероятностей выбора вариантов
- вектор условных вероятностей выбора вариантов ![]() в момент времени
в момент времени ![]() .
.
Выбору очередного варианта ![]() предшествует вычисление в соответствии с (6), вектора
предшествует вычисление в соответствии с (6), вектора ![]() . Вариант
. Вариант ![]() представляет собой случайную дискретную величину, принимающую значения
представляет собой случайную дискретную величину, принимающую значения ![]() с условными вероятностями
с условными вероятностями ![]() при фиксированной предыстории
при фиксированной предыстории ![]() .
.
Рандомизированные правила выбора (7) включают и так называемые марковские правила, которые можно описать как:
![]() ,
, ![]() (7)
(7)
Рандомизированные стратегии, определяемые последовательностью правил вида (7) относятся к классу рекуррентных алгоритмов адаптивного выбора вариантов. Эти алгоритмы достаточно просто реализуются, поскольку они на каждом шаге ![]() используют минимальную информацию о предыстории процесса.
используют минимальную информацию о предыстории процесса.
Применение рандомизированных стратегий позволит решать широкий класс задач адаптивного выбора вариантов, включая задачи с небинарными и с неограниченными потерями ![]() , более того, единообразно формировать алгоритм адаптивного выбора вариантов для всех рассматриваемых задач.
, более того, единообразно формировать алгоритм адаптивного выбора вариантов для всех рассматриваемых задач.
В условиях полной информации о системе оптимальная стратегия всегда принадлежит классу детерминированных стратегий:
![]() ,
, ![]() . (8)
. (8)
С помощью детерминированных стратегий может быть решено большинство задач УИР, возникающих в распределенных информационных системах.
Более простая реализация детерминированных стратегий возможна с помощью детерминированных конечных автоматов [8], которые в основном ориентированы на задачи с бинарными потерями, хотя могут применяться и в других случаях. Кроме того, для них характерно обеспечение приемлемого поведения, близость которого к оптимальному возрастает с увеличением глубины памяти автомата. Однако это влечет за собой уменьшение скорости достижения цели и увеличивает сложность, а именно число состояний, соответствующего автомата. Это же свойственно и стохастическим автоматам с постоянной структурой [9], которые реализуют рандомизированные стратегии выбора. Сложным рандомизированным стратегиям (6) и (7) в теории поведения автоматов соответствуют стохастические автоматы с переменной структурой.
Анализ наиболее распространенных стратегий адаптивного выбора вариантов позволил сформировать общий подход к созданию модели поведения автономного сценария в информационном пространстве с использованием конечных автоматов [9]. В соответствии с этим была предложена классификация автономных сценариев на основе фреймовой структуры. Для каждого класса используется бинарная функция потерь и определены стратегия поведения, условия функционирования и тип конечного автомата (см. табл.1).
Таблица № 1
Классы автономных сценариев
|
Характеристика |
Классы автономных сценариев |
||
|
Класс А |
Класс В |
Класс С |
|
|
Наличие информации о состоянии системы |
полная информация |
априорная неопределенность |
априорная неопределенность |
|
Функция потерь |
|
|
|
|
Стратегия поведения |
|
|
|
|
Модель поведения |
автоматная модель поведения типа «автомат-строка» |
автоматная модель поведения |
автоматная модель поведения |
|
Тип автомата |
детерминированный, стохастический с постоянной структурой |
детерминированный, стохастическиий с переменной структурой |
детерминированный, стохастическиий с переменной структурой |
|
Тип сценария |
рефлексивный, автономный |
автономный |
интеллектуальный |
Исследование выделенных классов позволяет формализовать их поведение в терминах теории конечных автоматов.
3 Модель поведения автономного сценария в терминах теории конечных автоматов
Конечный автомат рассматривается как некоторый объект [7 – 9], способный в каждый момент времени ![]() ,N воспринимать конечное число сигналов
,N воспринимать конечное число сигналов ![]() и изменять в зависимости от них свое внутреннее состояние. Автомат может производить конечное число действий
и изменять в зависимости от них свое внутреннее состояние. Автомат может производить конечное число действий ![]() , выбор действия определяется внутренним состоянием автомата. Автомат имеет конечное число m внутренних состояний
, выбор действия определяется внутренним состоянием автомата. Автомат имеет конечное число m внутренних состояний ![]() , которое называется емкостью памяти автомата.
, которое называется емкостью памяти автомата.
Предполагается, что автомат находится в некоторой среде и что действия ![]() автомата вызывают ответные реакции
автомата вызывают ответные реакции ![]() среды
среды ![]() . Эти реакции, в свою очередь, являются для автомата входными сигналами, которые он использует для принятия решения о дальнейших действиях (рис. 3).
. Эти реакции, в свою очередь, являются для автомата входными сигналами, которые он использует для принятия решения о дальнейших действиях (рис. 3).
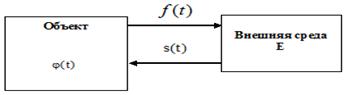
Рис.3 - Схема взаимодействия объекта с внешней средой
Рассмотрим простейший случай, когда все возможные реакции среды ![]() воспринимаются автоматом как относящиеся к одному из двух классов - классу благоприятных реакций (выигрыш,
воспринимаются автоматом как относящиеся к одному из двух классов - классу благоприятных реакций (выигрыш, ![]() ) и классу реакций неблагоприятных (проигрыш,
) и классу реакций неблагоприятных (проигрыш, ![]() ). Внутри каждого из этих классов реакции среды являются для автоматов неразличимыми. Целесообразность поведения автомата в некоторой среде заключается в увеличении числа благоприятных реакций и уменьшении числа реакций неблагоприятных.
). Внутри каждого из этих классов реакции среды являются для автоматов неразличимыми. Целесообразность поведения автомата в некоторой среде заключается в увеличении числа благоприятных реакций и уменьшении числа реакций неблагоприятных.
Ограничим наше исследование рассмотрением детерминированных и стохастических автоматов.
Автомат задается уравнением ![]() ,показывающим зависимость действия
,показывающим зависимость действия ![]() автомата в момент времени t от его состояния
автомата в момент времени t от его состояния ![]() , и стохастической матрицей
, и стохастической матрицей ![]() . При этом
. При этом ![]() равно вероятности перехода состояния
равно вероятности перехода состояния ![]() в состояние
в состояние ![]() под воздействием входа
под воздействием входа ![]() . Для детерминированных автоматов матрицы
. Для детерминированных автоматов матрицы ![]() состоят из нулей и единиц. Так как рассматриваются автоматы, воспринимающие лишь два сигнала
состоят из нулей и единиц. Так как рассматриваются автоматы, воспринимающие лишь два сигнала ![]() и
и ![]() , то достаточно задать две такие матрицы
, то достаточно задать две такие матрицы ![]() и
и ![]() . Таким образом, детерминированный автомат
. Таким образом, детерминированный автомат ![]() может быть задан каноническими уравнениями:
может быть задан каноническими уравнениями:
![]() , (9)
, (9)
![]() . (10)
. (10)
Уравнение (10) описывает зависимость действий автомата от его состояний, а уравнение (9) – изменения его состояний под воздействием входной переменной ![]() . Каждая строка матрицы состояний детерминированного автомата при любом фиксированном значении
. Каждая строка матрицы состояний детерминированного автомата при любом фиксированном значении ![]() содержит один элемент, равный 1, а остальные элементы равны 0. Смена состояний детерминированного автомата осуществляются в соответствии с правилом: если в момент
содержит один элемент, равный 1, а остальные элементы равны 0. Смена состояний детерминированного автомата осуществляются в соответствии с правилом: если в момент ![]() автомат находится в состоянии
автомат находится в состоянии ![]() , то в момент
, то в момент ![]() он перейдет в такое состояние
он перейдет в такое состояние ![]() , для которого
, для которого ![]() .
.
Стохастический автомат также имеет конечное число состояний ![]() и конечное число действий
и конечное число действий ![]() . Действия стохастического автомата однозначно определяются его состоянием:
. Действия стохастического автомата однозначно определяются его состоянием: ![]() , а матрицы состояний
, а матрицы состояний ![]() ,
, ![]() являются стохастическими. При этом
являются стохастическими. При этом ![]() имеет смысл вероятности перехода из i-го состояния в j-e при заданном значении входной переменной
имеет смысл вероятности перехода из i-го состояния в j-e при заданном значении входной переменной ![]() . Пусть в момент
. Пусть в момент ![]() автомат находится в состоянии
автомат находится в состоянии ![]() ,
, ![]() , которому соответствует действие
, которому соответствует действие ![]() . Тогда вероятность
. Тогда вероятность ![]() перехода автомата из состояния
перехода автомата из состояния ![]() в состояние
в состояние ![]() определяется формулой:
определяется формулой:
![]()
![]() . (11)
. (11)
Очевидно, что матрица ![]() является стохастической.
является стохастической.
С учетом общей модели поведения конечного автомата (10) и модели слота (2) и (3) представим автономный сценарий в терминах модели конечного автомата, тогда ![]() слотов
слотов ![]() соответствуют
соответствуют ![]() типам действий
типам действий ![]() :
:
![]()
![]()
![]() (12)
(12)
Каждый слот ![]() по аналогии с автоматом для i-го действия обладает конечным числом внутренних состояний
по аналогии с автоматом для i-го действия обладает конечным числом внутренних состояний ![]() :
:
![]()
![]()
![]() (13)
(13)
где n - количество слотов-заданий, m - количество состояний i-го кортежа-задания.
Тогда логическая модель автономного сценария примет вид, представленный на рис.4.
При выполнении условия, заданного форматом атрибута [CON], для объекта [OBG] выполняется встроенная процедура [PROC] или действие, определенное спецификацией [ACT]. На каждое действие среда отвечает сигналом ![]() , значение которого {1,0} отображается в поле [FLAG]. Накопленные в течение определенного периода результаты выполнения заданий, сформулированных в слотах-кортежах, могут быть использованы для моделирования адаптивного поведения сценариев. Ориентация на реакцию среды, в которой функционирует автономный сценарий, позволяет ему достичь поставленной цели. Конфликтные ситуации между сценариями разрешаются на основе приоритетов, заданных в поле [PRI].
, значение которого {1,0} отображается в поле [FLAG]. Накопленные в течение определенного периода результаты выполнения заданий, сформулированных в слотах-кортежах, могут быть использованы для моделирования адаптивного поведения сценариев. Ориентация на реакцию среды, в которой функционирует автономный сценарий, позволяет ему достичь поставленной цели. Конфликтные ситуации между сценариями разрешаются на основе приоритетов, заданных в поле [PRI].
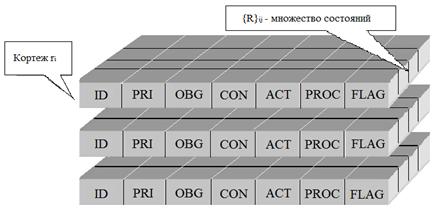
Рис.4. - Двумерная логическая модель автономного сценария
Таким образом, модель автономного сценария представляет собой сложную логическую структуру и как обязательный атрибут должна содержать имя фрейма-сценария, который включает слоты-задания ![]() (см. рис. 5).
(см. рис. 5).
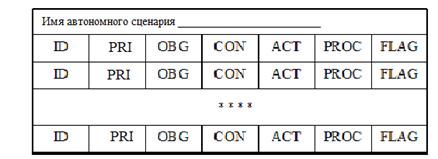
Рис.5. - Структура фрейма автономного сценария
|
|
|
… |
|
|
|
|
… |
|
Поведение автономного сценария определяется матрицей переходов, которая имеет вид:
Алгоритм автономного сценария состоит в следующем: задание, сформулированное в первом слоте-кортеже, выполняется ![]() раз, после чего управление передается на второй слот-кортеж. Задача считается полностью выполненной тогда, когда действие
раз, после чего управление передается на второй слот-кортеж. Задача считается полностью выполненной тогда, когда действие ![]() слота-кортежа выполнится
слота-кортежа выполнится ![]() раз.
раз.
В качестве примера рассмотрим автономный сценарий класса А, состоящий из одного слота и имеющий три состояния [10]. Сценарий активируется при наступлении конкретной даты (21 сентября 2011 года) и времени (17.00 часов системного времени) и копирует содержимое папки d:\arhiv\### на диск е:\ в одноименную папку (см.рис.6). Сценарий трижды выполняется в системе 21, 22 и 23 сентября. Результаты копирования заносятся либо в соответствующую таблицу БД, либо в текстовый файл (журнал).
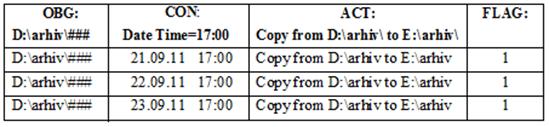
Рис.6.- Структура автономного сценария класса A
Если несколько изменить задание этого сценария, то есть не указать дату, а количество состояний задать равным 1, то копирование папки будет производиться ежедневно в 17.00 часов.
Выводы
Одним из перспективных направлений автоматизации процесса управления информационными ресурсами вычислительной системы является технология автономных сценариев, обеспечивающая решение широкого класса задач, таких как интеграция гетерогенных информационных структур и распределенных баз данных, мониторинг и автономный аудит информационных ресурсов. В статье предложена логическая модель автономных сценариев на основе фреймов, позволяющая формализовать как детерминированные, так и стохастические сценарии.
Для моделирования поведения автономных сценариев при взаимодействии с информационной средой предложено использовать аппарат конечных автоматов, позволяющий описать широкий спектр алгоритмов поведения, в том числе адаптивные и интеллектуальные. Разработанные модели повышают эффективность проектирования и сопровождения систем управления информационными ресурсами, являются основой для создания инструментального программного средства автоматизированного генерирования автономных сценариев.
Список литературы:
- Minsky, Marvin. A framework for representing knowledge. [Electronic resource] // MIT AI Laboratory Memo 306. June, 1974. -. Режим доступа: http://web.media.mit.edu/~minsky/papers/Frames/frames.html (доступ свободный) – Загл. с экрана. – Яз. англ.
- Chaib-draa, B., Moulin, B., Mandiau, R. & Millot, P. Chapter 1 - Trends in Distributed Artificial Intelligence, Foundations of Distributed Artificial Intelligence [Text] // G. M. P. O'Hare and N. R. Jennings (eds.), John Wiley & Sonsmc, 1996. - p. 3-55.
- Аксенов К.А. Коалиционная модель мультиагентного процесса преобразования ресурсов [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://ivdon.ru/magazine/issue/106 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Филатов В.А. Модель поведения автономного агента на основе теории автоматов [Текст] // Вестник Херсонского государственного технического университета.- Херсон: ХГТУ, 2004. - № 1 (19) - с.108 - 111.
- Трахтенброт Б.А., Барздинь Я.М. Конечные автоматы (поведение и синтез) [Текст] // Борис Трахтенброт, Ян Барздинь - М.: Мир, 1970. - с.400
- Кудрявцев В.Б., Введение в теорию автоматов [Текст] // В.Б. Кудрявцев, С.В. Алешин, А.С. Подколзин - М.: Наука, 1985. - с.319
- Назин А.В., Позняк А.С. Адаптивный выбор вариантов: рекуррентные алгоритмы [Текст] //А.В. Назин, С.В. Алешин - М.: Наука, Глав. ред. физико-математической лит-ры, 1986. - с.288, ил., 21 см.
- Цетлин М. Л. Исследования по теории автоматов и моделированию биологических систем [Текст] // М.Л. Цетлин - М.: "Наука", 1969 - с.316
- Филатов В.А., Козырь О.Ф. Мультиагентный подход к идентификации пользователей в системе дистанционного образования [Текст] // Сборник трудов региональной научной конференции,- Старый Оскол ООО "ТНТ", 2005. – т.1- c. 284-290.
- Ананьев А.С., Бутенко Д.В., Попов К.В. Интеллектуальные технологии проектирования информационных систем. Методика проектирования программных продуктов в условиях наличия прототипа [Электронный ресурс] // «Инженерный вестник Дона», 2012, №2. – Режим доступа: http://ivdon.ru/magazine/issue/103 (доступ свободный) – Загл. с экрана. – Яз. рус.