Повышение точности калибровки внешних параметров видеокамеры
Аннотация
Дата поступления статьи: 14.09.2013Описана модель идеальной видеокамеры, показан вид внешних и внутренних параметров камеры. Приведены соотношения, связывающие координаты точки в мировой системе координат с координатами проекции этой точки на изображение. Поставлена задача определения внешних параметров камеры по набору соответствий точек в мировой системе координат и их проекций на изображение. С помощью моделирования оценены погрешности определения внешних параметров камеры для различных конфигураций калибровочных объектов. По результатам моделирования даны рекомендации по выбору параметров калибровочного объекта с целью увеличения точности калибровки внешних параметров видеокамеры.
Ключевые слова: калибровка видеокамеры, внешние параметры камеры, оценка положения и ориентации, калибровочный объект
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Во многих задачах компьютерного зрения, например при построении систем стереовидения [1], систем видеорегистрирования, а также при визуализации моделируемых объектов на изображении [2], возникает необходимость оценки положения видеокамеры в пространстве по полученным ею изображениям известного калибровочного объекта. Стремительное развитие фото - и видеорегистрирующей аппаратуры повышает требования к точности определения калибровочных параметров и вызывает необходимость произвести исследование влияния выбора параметров калибровочного объекта на точность калибровки.
Связь между координатами точки в мировой системе координат (СК) x = (x, y, z) и ее проекции на изображение p = (u, v) описывается с помощью выражения
![]() ,
,
где K – матрица внутренних параметров камеры, позволяющая перейти от координат точки в СК камеры к координатам проекции этой точки на изображении; [R | t] – внешние параметры камеры, определяющие переход из мировой СК к СК камеры, ![]() – однородные координаты точки на изображении.
– однородные координаты точки на изображении.
Внутренние параметры уникальны для каждой камеры и не зависят от других камер и положения в пространстве. Их можно определить индивидуально для каждой камеры с помощью геометрической калибровки по методике, описанной в [3, 4]. При отсутствии геометрических искажений внутренние параметры камеры записываются в виде матрицы камеры:
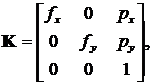
где fx, fy – фокусные расстояния камеры, px, py – координаты точки пересечения оптической оси и плоскости изображения в системе координат изображения.
Внешние параметры камеры имеют вид
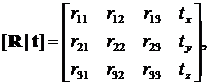
где R = [rij] – матрица поворота размера 3 × 3, задающая ориентацию камеры и имеющая три степени свободы; t = (tx, ty, tz) – вектор переноса, совмещающий начала мировой СК и СК камеры.
Для определения внешних параметров камеры после калибровки внутренних параметров достаточно иметь набор как минимум из четырех соответствий между координатами точек в пространстве xi = (xi, yi, zi) и координатами точек на изображении pi = (ui, vi). Такая задача популярна в области компьютерного зрения и может решаться различными методами, в основном отличающимися вычислительной сложностью [5–7].
В библиотеке OpenCV также имеется реализация такой функции с именем cv::solvePnP или cvFindExtrinsicCameraParams2 в случае старого интерфейса [8, с. 395]. В качестве входных параметров в эту функцию поступают: массив трехмерных точек пространства, соответствующий этим точкам массив двумерных точек на изображении, внутренние параметры камеры (матрица камеры и коэффициенты дисторсии). Выходными параметры этой функции являются вектор переноса t = (tx, ty, tz) и вектор вращения w = (wx, wy, wz) . Вектор вращения является описанием поворота в пространстве на угол θ = ||w|| вокруг единичного вектора u = w / θ. Матрица вращения может быть получена из u и θ с помощью формулы Родрига [9, с. 38]:
R(u, θ) = I + sin θ [u]× + (1 – cos θ) [u]×2,
где I – единичная матрица 3×3, а [u]× – кососимметричная матрица, используемая для обозначения векторного произведения:
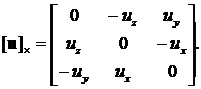
На практике вместо вектора переноса t удобно оперировать положением камеры c = (cx, cy, cz) , которое при известных R и t находится по следующей формуле (обратная матрица поворота получается транспонированием матрицы прямого поворота R−1 = RT):
с = − RT t.
Ориентацию камеры удобно задавать в виде последовательности элементарных вращений r = (λ, φ, θ) на углы азимута, высоты и крена соответственно, которые для известной матрицы поворота R = [rij] можно найти по следующим формулам [10]:
λ = arctan2(r31, r32),
φ = arcsin(r33),
θ = arctan2(–r13, –r23),
где arctan2(x, y) – двухаргументная функция арктангенса, эквивалентная функции arctan(y / x) с учетом четверти, в которой находится точка (x, y), принимающая значения в интервале (–π, π].
При помощи моделирования выполнено исследование того, как влияет выбор и погрешность измерения пространственных координат x и соответствующих двумерных координат p на точность оценки положения камеры. Моделировалась камера с углом обзора по горизонтали α = 68° и разрешением изображения w × h = 704 × 576 пикселей. Внутренние параметры камеры, таким образом, были приняты следующими:
fx = fy = w / (2 tan(α/2) ) ≈ 521,9;
px = (w – 1) / 2 = 351,5;
py = (h – 1) / 2 = 288,5;
Внешние параметры камеры задавались следующим образом: камера располагалась в начале координат c0 = (0, 0, 0), а углы ее ориентации были приняты нулевыми c0 = (0, 0, 0) (направление оси Z СК камеры совпадает с направлением оси Y мировой СК):
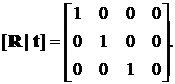
Точки в мировой СК определяются выбором калибровочного объекта. Исследовалось несколько конфигураций точек xi калибровочного объекта с различными расстояниями от камеры и различными угловыми размерами (таблица 1):
1. Конфигурация из четырех точек, проекции которых разнесены друг от друга и расположены в угловых областях изображения.
2. Конфигурация из четырех точек, проекции которых не сильно разнесены друг от друга.
3. Конфигурация из восьми точек, полученная объединением 1-й и 2-й конфигурации.
4. Конфигурация из четырех точек, расположенных дальше от камеры, чем во второй конфигурации, проекции которых также расположены по углам изображения.
5. Конфигурация из четырех точек, составленная из 1-й и 4-й конфигураций (из каждой взято по две точки).
Таблица №1
Конфигурации точек и их проекции
x, м |
p, пикс. |
x, м |
p, пикс. |
||||||
|
Конфигурация № 1 |
Конфигурация № 2 |
||||||||
|
Конфигурация № 3 |
|||||||||
|
−1 |
2 |
1 |
90,6 |
26,6 |
−0,5 |
2 |
0,5 |
221,0 |
157,0 |
|
1 |
2 |
1 |
612,4 |
26,6 |
0,5 |
2 |
0,5 |
482,0 |
157,0 |
|
−1 |
2 |
−1 |
90,6 |
548,4 |
−0,5 |
2 |
−0,5 |
221,0 |
418,0 |
|
1 |
2 |
−1 |
612,4 |
548,4 |
0,5 |
2 |
−0,5 |
482,0 |
418,0 |
|
Конфигурация № 4 |
Конфигурация № 5 |
||||||||
|
−2 |
4 |
2 |
90,6 |
26,6 |
−2 |
4 |
2 |
90,6 |
26,6 |
|
2 |
4 |
2 |
612,4 |
26,6 |
2 |
4 |
2 |
612,4 |
26,6 |
|
−2 |
4 |
−2 |
90,6 |
548,4 |
−1 |
2 |
−1 |
90,6 |
548,4 |
|
2 |
4 |
−2 |
612,4 |
548,4 |
1 |
2 |
−1 |
612,4 |
548,4 |
Моделировалась погрешность оценки пространственных координат ±ex = 1, 5 и 10 мм и погрешность определения координат на изображении ±ep= 1 пиксель. Для этого к каждой пространственной координате x добавлялась случайная ошибка ξ с нормальным законом распределения и среднеквадратичным отклонением σx = ex/2, что соответствует доверительному интервалу 95% для заданного ex. Затем полученные зашумленные координаты xξ = x + ξ(σx) проецировались на изображение, и к найденным проекциям добавлялся гауссов шум с среднеквадратичным отклонением σp = ep/2:
![]() .
.
Для полученных таким образом соответствий ![]() и x с помощью функции solvePnP библиотеки OpenCV определялись внешние параметры камеры, а затем находились положение ci и ориентация ri камеры, где i = 0, 1, … N, N = 1000 – число, достаточное для статистически достоверной оценки погрешности.
и x с помощью функции solvePnP библиотеки OpenCV определялись внешние параметры камеры, а затем находились положение ci и ориентация ri камеры, где i = 0, 1, … N, N = 1000 – число, достаточное для статистически достоверной оценки погрешности.
Ошибка определения положения камеры для 95-процентного доверительного интервала находилась как два среднеквадратичных отклонения xi от x0:
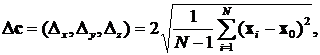
аналогично определялась ошибка определения ориентации Δr = (Δλ, Δφ, Δθ). Рассчитанные таким образом погрешности приведены в таблице 2.
Таблица № 2
Значения ошибки определения положения Δx и ориентации Δr камеры в зависимости от ошибки измерения пространственных координат ex для различных конфигураций.
ex, мм |
Δx, мм |
Δr |
||||
|
Конфигурация № 1 |
||||||
|
1 |
5,6 |
5,6 |
1,6 |
0,13° |
0,13° |
0,04° |
|
5 |
14,6 |
14,4 |
4,5 |
0,34° |
0,33° |
0,11° |
|
10 |
26,9 |
27,9 |
8,8 |
0,62° |
0,65° |
0,21° |
|
Конфигурация № 2 |
||||||
|
1 |
18,8 |
18,3 |
3,1 |
0,50° |
0,49° |
0,09° |
|
5 |
47,8 |
45,2 |
8,2 |
1,28° |
1,22° |
0,21° |
|
10 |
91,6 |
88,6 |
15,3 |
2,48° |
2,40° |
0,43° |
|
Конфигурация № 3 |
||||||
|
1 |
4,4 |
4,5 |
1,5 |
0,11° |
0,11° |
0,04° |
|
5 |
12,0 |
12,0 |
4,0 |
0,30° |
0,30° |
0,10° |
|
10 |
23,8 |
23,1 |
7,8 |
0,59° |
0,58° |
0,18° |
|
Конфигурация № 4 |
||||||
|
1 |
10,3 |
10,2 |
2,8 |
0,12° |
0,12° |
0,04° |
|
5 |
16,5 |
16,0 |
5,3 |
0,19° |
0,18° |
0,06° |
|
10 |
29,2 |
28,1 |
9,5 |
0,34° |
0,33° |
0,11° |
|
Конфигурация № 5 |
||||||
|
1 |
4,4 |
4,1 |
2,3 |
0,08° |
0,07° |
0,05° |
|
5 |
9,2 |
10,4 |
6,1 |
0,14° |
0,16° |
0,09° |
|
10 |
16,8 |
19,4 |
11,9 |
0,26° |
0,29° |
0,17° |
По результатам моделирования можно сделать следующие рекомендации:
1. Для уменьшения погрешностей необходимо увеличивать угловое расстояние между проекциями точек (конфигурации №1 и №2)
2. Добавление дополнительных точек позволяет уменьшить погрешность (конфигурации №1 и №3)
3. Отдаление точек в пространстве без изменения их угловых расстояний уменьшает погрешность определения ориентации камеры, но увеличивает погрешность определения положения камеры (конфигурации №1 и №4)
4. Предпочтительно располагать точки в пространстве так, чтобы они имели различные дальностные координаты. В этом случае погрешности распределяются более равномерно для различных координат или осей поворота, и их суммарное значение в этом случае наименьшее (конфигурации №1 и №5).
5. Предполагается достаточно точным определение положения и ориентации камер с точностью измерения пространственных координат 10 мм, для конфигурации из четырех разноудаленных от камеры точек (конфигурация №5).
Литература:
1. Лахов, А.Я. Программное обеспечение для стереовизуализации результатов конечно-элементного моделирования [Электронный ресурс] // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2013/1501 (доступ свободный) – Загл. с экрана. – Яз. рус.
2. Рачковская Г.С. Математическое моделирование и компьютерная визуализации сложных геометрических форм // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2013/1498 (доступ свободный) – Загл. с экрана. – Яз. рус.
3. Sturm Peter F, Maybank Stephen J. On plane-based camera calibration: A general algorithm, singularities, applications // Computer Vision and Pattern Recognition, 1999. IEEE Computer Society Conference on. / IEEE. –Vol. 1. – 1999.
4. Zhang Zh. A Flexible New Technique for Camera Calibration // IEEE Transactions on Pattern Analysis and Machine Intelligence. – 2000. – Vol. 22(11). – P. 1330– 1334.
5. Complete Solution Classification for the Perspective-Three-Point Problem / XiaoShan Gao, Xiao-Rong Hou, Jianliang Tang, Hang-Fei Cheng // IEEE Transactionson Pattern Analysis and Machine Intelligence. – 2003. – Vol. 25, no. 8. – P. 930–943.
6. Moreno-Noguer F., Lepetit V., Fua P. Accurate Non-Iterative O(n) Solution to the PnP Problem // Computer Vision, 2007. ICCV 2007. IEEE 11th International Conference on. – 2007. – P. 1–8.
7. Schweighofer Gerald, Pinz Axel. Globally Optimal O(n) Solution to the PnPProblem for General Camera Models. // BMVC. – 2008. – P. 1–10.
8. Bradski Gary, Kaehler Adrian. Learning OpenCV. – Sebastopol: O’Reilly, 2008. – 555 p.
9. Szeliski R. Computer Vision. Algorithms and Applications / Ed. by D. Gries, F. B. Schneider. – Springer, 2011. – 812 p.
10. Толкачев Д.С. Преобразования координат, связанные с вращением камеры, при формировании панорамы. – Материалы Всероссийской научной конференции «Инновационные процессе в гуманитарных, естественных и технических системах» – часть 3 – Таганрог: Изд-во ТТИ ЮФУ, 2012 г, с. 68–72.