Метод оценки прочности металла неразрушающим способом с использованием априорной информации

Аннотация

Н.Л. Вернези

Дата поступления статьи: 18.09.2013

Рассмотрены  вопросы, связанные с оценкой механических свойств стальных  элементов строительных металлоконструкций. Измерения производятся неразрушающим методом на основе анализа характеристик внедрения конического индентора  в поверхность материалла. Такой метод  позволяет оперативно  получать значения всех механических  характеристик металла.   При этом измерения механических характеристик  можно производить к в любой точке конструкции. В то же время, при больших размерах  конструкции и больших объемах измерительных  работ, необходимо  оценить  достаточное  количества измерений в  конкретном  месте.  Предложен и реализован байесовский метод  учета априорной информации  для снижения числа измерений и трудоемкости процесса получения механических характеристик.

Ключевые слова: неразрушающий контроль, механические характеристики, прочность, диагностика, априорная информация, испытания металла.

В случае необходимости реконструкции бывшего в эксплуатации сооружения важно провести диагностику его состояния с точки зрения прочностного ресурса, поскольку с течением времени эксплуатации металл изменяет свои механические характеристики [1,2], а реконструкция, как правило, приводит к перераспределению сил, действующих  в элементах будущего сооружения. В соответствии с [3]при исследовании ииспытании металла необходимо оценить предел текучести, предел прочностии относительное удлинение. При этом количество элементов, проверяемых в партии должно быть не менее двух, образцов от каждого элемента не менее двух от всей партии. Однако, в определенных случаях [4] запрещается применение разрушающих методов прочности металла, получить знание можно только методами неразрушающего контроля. Один из них лежит в основе, разработанной в РГСУ системы безобразцовой оценки механических свойств «Прочность»[5,6,7,8,9], основанный на ударном внедрении конического индентора в испытуемый металл. При этом значение механической характеристики  (МХ) определяется в любой его точке. Такая оценка имеет суммарное рассеивание, обусловленное реальным разбросом свойств в объеме металла и погрешностью измерения.
Разброс значений МХ, полученных стандартными разрушающими методами испытаний образцов одной партии металла, может достигать
±10% и более. Проведенные исследования по определению погрешности измерения системой «Прочность» МХ в различных точках единичных образцов показали предельные ее значения в границах ± 8%. Суммарное рассеивание значений МХ имеет вероятностный характер и наилучшим образом может быть описано трехпараметрическим законом распределения Вейбулла[10,11,12,13,14].Этот закон имеет несомненное преимущество, поскольку дает информацию о сдвиге распределения или минимальном значении  МХ. Вместе с тем, нормальный закон часто используется вследствие большого удобства применения и наличия в виде параметров как математического ожидания механической характеристики, так и ее среднеквадратичного отклонения.
Неразрушающий контроль МХ удобен, оперативен, прост. Однако остается открытым вопрос достаточного  количества измерений в данном  месте, особенно в случае масштабного обследования больших объемов металлоконструкций, а также в труднодоступных местах (например, на большой высоте), где бывает сложно произвести даже 1-2 измерения.
В этом случае неоценимую помощь может оказать применение байесовских процедур на основе использования априорной информации, Апостериорная плотность распределения параметра измеряемой случайной величиныпо Байесу выражается:
(1)

где:  – плотность априорного распределения параметра или доопытное знание о принимаемых им значениях;
- плотность априорного распределения параметра или доопытное знание о его возможных значениях
 – функция правдоподобия или условная плотность распределения полученных значений  при  данном значении .
Практическое применение формулы (1)облегчается при условии сопряженности и [15, 16].
Этот момент можно обойти, приняв в качестве не мгновенное, а среднее значение параметра , тогда в соответствии с центральной предельной теоремойи и можно принять нормально распределенными и апостериорная плотность распределения параметра

выразится:,
где:–средние значения измеряемой опытной величины, и – соответственно их математическое ожидание и среднеквадратичное отклонение. При этом будет также иметь нормальный вид, а апостериорные оценки среднего

и среднеквадратичного отклоненияпримут вид:

;
;

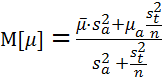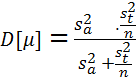где:  - выборочная средняя измеренных случайных величин;
–математическое ожидание случайной величины;
и- соответственно среднеквадратичные отклонения среднего значения случайной измеряемой величины оти  от;
Необходимое число измерений n определится:
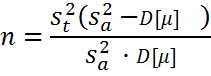(2)
Натурный эксперимент по оценке МХ при обследовании реконструируемого здания в г. Батайске по ул. 1 Пятилетки выявил следующее. Средние значения предела прочности металла класса С285 марки Ст.3 имели размах 137 МПа. Это позволило, используя правило трех сигм, задаться значением = 23МПа. Значением= 3МПа задались в предположении, что размах может находиться в границах 10 МПа.
Значение  принято из регламентированного размаха значения временного сопротивления для сталей класса С285 [17]380-400МПа.
Расчет по формуле(2)показал, что достаточным при этих значениях исходных данных являются всего 2-3 измерения.

Литература:

1. Природа усталости металлов. Иванова В.С., Терентьева В.Ф. – М. «Металлургия», 1975 – 456с.
2. Горицкий В.М. Диагностика металлов. – М.: Металлургиздат, 2004. – 408с.
3.  СНиП II-23-81*. Стальные конструкции. -М. Госстандарт,1988, 113с.
4.СП 13-102-2003. Правила обследования несущих строительных  конструкций зданий и сооружений. -М. Госстрой, 2004, 24с.
5. D.M. Belen’kii, A.N. Beskopyl’nyi, N.L. Vernezi, L.G. Chamraev. Determination of the strength of butt welded joints // Welding International.
1997.- №11.С.643-645.
6. D.M. Belen’kii, N.L. Vernezi, A.V. Cherpakov. Changes in the mechanical  properties of butt welded joints in elastoplastic  deformation//Welding International. 2004.- №18 (p.213-215).
7. Беленький Д.М., Бескопыльный А.Н., Вернези Н.Л. Опыт диагностики металлических  конструкций // Изв. вузов. Строительство. 2003. №1. С.99-102.
8. Вернези Н.Л. Применение системы «Прочность» при диагностике металлических конструкций// Изв. Ростовского государственного  строительного университета. 2003. №7. С. 56-60.
9. Вернези Н.Л., Веремеенко А.А. Диагностика прочности металлических конструкций.// Изв. Ростовского  государственного строительного  университета.  2012. №17.
10. Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648с.
11. W.J. DeCoursey / Statistics and Probability for Engineering Applications With Microsoft® Excel. – 2003 – 400 р. – Elsevier Science (USA).
12. Серенсен С.В., Кагаев В.П., Шнейдерович Р.М. Несущая способность и расчеты деталей машин на прочность. – М.: Машиностроение, 1975. – 488с.
13. Касьянов В.Е., Котесов А.А., Котесова А.А. Аналитическое определение параметров закона Вейбулла для генеральной совокупности конечного объема по выборочным данным прочности стали [Электронный ресурс] // «Инженерный вестник Дона», 2012, №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2012/804(доступ свободный) – Загл. с экрана. – Яз.рус.
14. Касьянов В.Е., Щулькин Л.П., Котесова А.А., Котова С.В / Алгоритм определения параметров прочности, нагруженности и ресурса с помощью аналитического перехода от выборочных данных к данным совокупности [Электронный ресурс] // «Инженерный вестник Дона», 2012,
№4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1236 (доступ свободный) – Загл. с экрана. – Яз.рус.
15. Кокс Д., Хинкли Д. Теоретическая статистика. - М.: Мир, 1978.- 500с.
16. М. Де Гроот. Оптимальные статистические решения. - М.: Мир, 1974.- 491 с.
17. Металлические конструкции. В 3 т. Т. 1. Элементы стальныхконстркций: Учеб. Пособие для строит.вузов/В.В.Горев, Б.Ю.Уваров, В.В.Филиппов и   др.; Под ред. В.В.Горева – М.: Высш. шк., 1997. – 527с.