Погонная индуктивность цилиндрических проводников с аксиальной плотностью тока в сложных функциональных блоках

Аннотация

В. Г. Сапогин, Н.Н. Прокопенко, В.В. Марчук, В.Г. Манжула

Предложен аналитический метод расчёта магнитных свойств круглого и полого бесконечно длинных цилиндрических проводников. Метод позволяет: рассчитать радиальные распределения векторного потенциала и индукции магнитных полей, формируемых во внутренней и внешней областях проводника постоянным током; определить величины магнитных потоков во внутренней и внешней областях проводника; вычислить токовую и потоковую погонные индуктивности круглого и полого проводников; найти частотную зависимость добротности цилиндрических проводников и определить масштабы характеристических частот.

Ключевые слова: индуктивность, распределение магнитных полей, магнитный поток, добротность, сложный функциональный блок

Введение
В [1] был предложен аналитический метод расчёта потоковой индуктивности токового кольца с конечной радиальной шириной, который основывался на законе Био-Савара-Лапласа для геометрического проводника [2].
Автоматизированный синтез сложных функциональных блоков [3-7] и IP-модулей систем связи и телекоммуникаций требует наличия результатов анализа распределения магнитных полей проводников с учетом конечности поперечного сечения проводника.
Сохраняя идеологию методики расчёта, предложенной в [1], рассчитаем погонную индуктивность цилиндрического проводника с аксиальной плотностью тока.
Распределение магнитных полей бесконечно длинного круглого проводника с током
Расчёт будем проводить исходя из фундаментального уравнения магнитостатики, записанного для векторного потенциала
,  (1)
с калибровкой
 .  (2)
Связь индукции магнитного поля с векторным потенциалом находится из соотношения
(3)
Запишем (1) в цилиндрических координатах с учётом того, что плотность тока имеет только одну аксиальную компоненту, направленную по оси z: . Она порождает поле векторного потенциала, имеющего также только одну компоненту  
.  (4)
Оператор Лапласа для декартовой компоненты векторного потенциала, зависящей от радиуса, имеет вид
.  (5)
Предположим, что в (5) плотность тока однородна по поперечному сечению , а проводник имеет конечный радиус R.
Из (3) следует, что такое поле векторного потенциала порождает индукцию магнитного поля с одной компонентой
.    (6)
Цилиндрическая поверхность проводника, имеющего радиус R, делит всё пространство, в котором возбуждено статическое магнитное поле, на две области: внутреннюю область (), в которой есть ток; и внешнюю область (), где тока нет. Поставленная задача очень похожа на задачу электростатики для уравнения Пуассона (внутренняя краевая задача).
Тогда для внутренней области (потенциал отмечен индексом «1») уравнение (5) имеет вид
,    (7)
а во внешней области (потенциал отмечен индексом «2») –
.   (8)
В уравнении (5) перейдём к новой функции , где , а
      (9)
- масштаб векторного потенциала.
Решение для внутренней области (7) имеет вид
,   (10)
а для внешней области (8)
,   (11)
где с₁,с₂,с₃,с₄ – произвольные постоянные. В решении (10) убираем особенность в нуле и выбираем нуль потенциала на оси системы . В этом заключается принципиальное отличие поставленной краевой магнитостатической задачи от электростатической. С учётом этого, получаем с₁=с₂=0.
Постоянные с₃ и с₄ определяем из условия непрерывности функции и её производной на границе областей . Окончательно решения (10) и (11) примут вид
 ,    (12)
Радиальное распределение индукции находим из (6)
,    (13)
где - масштаб индукции поля. 
Индукция линейно растёт во внутренней области
,   (14)
а во внешней области убывает по закону
.   (15)
Индуктивность круглого проводника
Наличие двух областей, в которых магнитное поле распределено по разным законам  указывает на то, что индуктивность прямолинейного круглого тока складывается из двух частей. Первая часть соответствует индуктивности, которая связана с потоком магнитного поля во внутренней области. В ней силовые линии магнитного поля поперечны линиям плотности тока. В связи с этим её удобно назвать токовой частью индуктивности.
Вторая часть соответствует индуктивности, которая связана с магнитным потоком, находящимся во внешней области. Её удобно назвать потоковой частью индуктивности.
Если цилиндрический проводник разрезать по оси (см. рис. 1), то видна область, по которой следует интегрировать при вычислении потока во внутренней области. На рис. 1 крестиками указано направление магнитных силовых линий при условии, что плотность тока направлена вдоль оси z. Ось проводника обозначена ОО’, а элементарная площадка интегрирования dS – заштрихована.
Вычисляя внутренний поток, получим
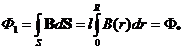, (16)
где - масштаб потока.
Учитывая соотношение (9) и связь , получим для погонной токовой части индуктивности выражение
. (17)
Как видно из (17), она не зависит от радиуса проводника и с точностью до константы совпадает с магнитной постоянной.

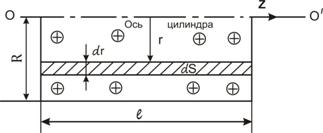
Рис. 1. - Площадка интегрирования при вычислении потока во внутренней области

Проводя аналогичные вычисления во внешней области, получим погонную потоковую индуктивность
. (18)
При вычислении (18) введён радиус обрезания магнитного поля r₀>R. Из (18) видно, что потоковая погонная индуктивность также не зависит от радиуса проводника, но имеет логарифмическую расходимость при .
Полная погонная индуктивность, выраженная через токовую индуктивность, имеет вид
     (19)
и также имеет логарифмическую расходимость при .
Зависимость полной погонной индуктивности цилиндрического проводника  от приведённого радиуса обрезания поля  представлена на рис. 2.

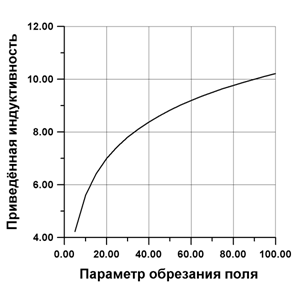
Рис. 2. - Зависимость приведённой индуктивности от параметра обрезания поля

Из рис. 2 видно, что при изменении параметра  ξ₀  в интервале от 5 до 100 приведённая полная индуктивность изменяется в пределах . Это говорит о том, что полная погонная индуктивность может в несколько раз превышать токовую индуктивность того же проводника.
Причина, по которой проявляется логарифмическая расходимость полной индуктивности, прозрачна. Решение поставленной задачи удаётся найти для бесконечно длинного проводника (отсутствует зависимость полей от переменной z).
Все реальные проводники, используемые в планарных технологиях, имеют конечную длину. Поэтому точное значение параметра обрезания поля и его зависимость от радиуса и длины проводника ждёт своего экспериментального определения.
Распределение магнитных полей бесконечно длинного трубчатого проводника с током
Для нахождения распределения магнитных полей трубчатого проводника воспользуемся уравнением (5). На рис. 3 представлена геометрия внешней краевой задачи.

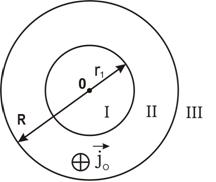
Рис. 3. - Геометрические параметры поперечного сечения трубчатого проводника

Предположим, что в (5) плотность тока однородна по поперечному сечению в проводящей области II, ограниченной неравенством . На рис. 3 r₁ – радиус полости, R – внешний радиус проводящей области, а направление вектора плотности тока обозначено крестиком.
Тогда для областей I и III, в которых нет тока, уравнение (5) приводится к виду
     (20)
а в области II, где течёт ток
.  (21)
Сохраняя те же значения масштабов векторного потенциала A* и индукции магнитного поля B*, выпишем решение для областей:
- для области I
;    (22)
- для области II
; (23)
- для области III
.   (24)
В (22) – (24) с₁, с₂, с₃, с₄, с₅, с₆ – произвольные постоянные. В решении (22) убираем особенность на оси и задаём нулевое значение потенциала у1(0)=0. 
С учетом этого, получаем c₁=c₂=0. Постоянные с₃ и с₄ определяем из условия непрерывности функции и её производной на первой границе : , . Постоянные с₅ и с₆ определяем из подобных условий на границе ξ=1: .
Радиальные распределения индукции находим из решений, полученных для потенциала (22) – (24) с учётом (13):
- в области I
;   (25)
- в области II
,  (26)
- области III
.   (27)
Графики радиального распределения приведённой индукции  от приведённой радиальной координаты ξ для трёх значений приведённого радиуса полости ξ₁=0,2 (кривая 1); ξ₂=0,5 (кривая 2); ξ₃=0,75 (кривая 3) представлены на рис. 4.

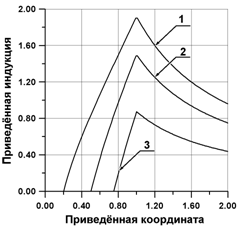
Рис.4. - Радиальное распределение приведённой индукции магнитного поля от приведенной координаты

Из рис. 4 видно, что магнитное поле внутри полости отсутствует, а производная индукции магнитного поля при переходе через внешнюю границу раздела испытывает скачок от значения  до значения .
Индуктивность трубчатого проводника
Наличие трёх областей, в которых магнитное поле распределено по разным законам, указывает на то, что индуктивность прямолинейного трубчатого тока также складывается из двух частей. Первая часть индуктивности, определяемая областью II, является токовой. Вторая часть индуктивности, связанная с магнитным потоком во внешней области, ─ потоковая.
Вычисляя потоки в соответствующих областях, получим:
- в области II
;   (28)
- в области III
.    (29)
В (29) по аналогии с (18) введено обозначение - приведённый радиус обрезания магнитного поля в области III.
Вычисляем соответствующие потокам погонные индуктивности:
- токовая индуктивность
 ;   (30)
- потоковая индуктивность
 .   (31)
Полная индуктивность единицы длины трубчатого проводника имеет вид
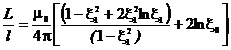.  (32)
Графики зависимости приведённой погонной токовой индуктивности (30) трубчатого проводника   от приведённого радиуса полости ξ₁ приведены на рис. 5. Из графика видно, что при малых значениях приведённого радиуса полости ξ₁ её значение совпадает со значением (17), полученным для круглого проводника. Поскольку функция (30) не может быть разложена в ряд по малому параметру ξ₁, то для этой области малых значений занесём значения приведённой индуктивности с точностью до пятого знака после запятой в табл. 1.

Таблица №1
Значения токовой индуктивности для малых значений приведённого радиуса полости

	0,01	0,02	0,03	0,04	0,05
	0,99908	0,99687	0,99368	0,98968	0,98498
	0,06	0,07	0,08	0,09	0,10
	0,97967	0,97381	0,96746	0,96067	0,95348

Введём параметр толщины стенки трубчатого проводника
.   (33)
Для проводника с тонкой стенкой (реализуются малые значения приведённой толщины трубки ) значения индуктивности можно вычислять из ряда по t, который быстро сходится:
. (34)

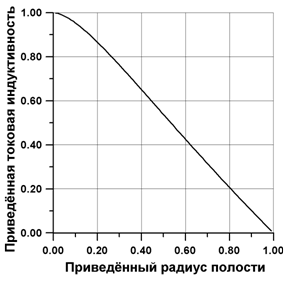
Рис. 5. - Зависимость погонной токовой индуктивности от радиуса полости

Из соотношения (34) видно, что значение токовой индуктивности становится линейной функцией приведённой толщины трубки при выполнении условия . Отсюда следует: чем меньше толщина трубчатого проводника, тем меньше значение его погонной токовой индуктивности
.   (35)
Как следует из (32), полная погонная индуктивность трубчатого проводника также имеет логарифмическую расходимость по параметру обрезания поля .  И в этом случае, точное значение параметра обрезания и его зависимость от радиуса и длины проводника ждёт своего экспериментального определения.
Добротность индуктивности цилиндрического проводника
Теоретическое значение индуктивности (32) следует считать индуктивностью на постоянном токе. Она остаётся неизменной для переменного тока в той области частот, когда фазовый сдвиг между током и потоком равен нулю. Для этой области частот такая индуктивность не зависит от частоты.
Рассчитаем зависимость добротности индуктивности от частоты и определим интервал частот, в котором она имеет приемлемые значения
,   (36)
где
   (37)
омическое сопротивление участка трубчатого проводника длиной l, ρ – удельное сопротивление проводника. Подставляя (37) в (36), получим
,  (38)
где ─ масштаб характеристической частоты
(39)
Как видно из (38), добротность полной индуктивности цилиндрического проводника не зависит от длины проводника, но зависит от частоты, приведённого радиуса полости и имеет логарифмическую расходимость по параметру обрезания поля при .
Нижняя характеристическая частота следует из (38) при Q=1
.   (40)
Добротность токовой индуктивности также зависит от частоты и приведённого радиуса полости ξ₁:
.   (41)
Нижняя характеристическая частота токовой индуктивности имеет вид
.  (42)
Как видно из (42), она, для одинаковых трубчатых проводников, будет тем выше, чем больше её удельное сопротивление.
Оценим добротность и нижнюю характеристическую частоту токовой индуктивности для круглого полого цилиндрического проводника со следующими параметрами: внешний радиус 5 мкм, удельное сопротивление 16 нОм·м (медь), радиус полости 1 мкм. Из оценки следует, что добротность токовой индуктивности из меди будет больше единицы для частот 0,38 Ггц, что по порядку величины сходится со значением нижней характеристической частоты для медного кольца в [1]. Для полого проводника с ξ₁=0,5 значение нижней характеристической частоты увеличивается в 2 раза.
Оценим границу применимости полученных результатов на высоких частотах. Её можно получить, исследуя времена установления неоднородных магнитных полей в трубчатом проводнике. Будем считать, что эти времена связаны со скоростью передачи электромагнитных взаимодействий - скоростью света. Тогда характерное время установления , где R – внешний радиус проводника, даёт значение верхней характеристической частоты . Вычисленное её значение для проводника радиусом 5 мкм получается 60×10¹² Гц. На современном этапе развития интегральных технологий эти частоты пока не достигнуты.

Выводы

• Предложен аналитический метод расчёта статических магнитных полей круглого и полого цилиндрических проводников с аксиальной плотностью тока.
• Радиальное распределение магнитного поля внутри проводника с током таково, что его индукция изменяется от нулевых и достигает конечных значений на внешней поверхности проводника.
• Радиальное распределение магнитного поля вне проводника с током таково, что оно всегда убывает при перемещении точки наблюдения от поверхности проводника наружу.
• Производная индукции магнитного поля при переходе через внешнюю границу раздела испытывает скачок.
• Теория показывает, что погонная индуктивность цилиндрического проводника состоит из двух составляющих: токовой погонной индуктивности и потоковой.
• Погонная токовая индуктивность трубчатого проводника становится линейной функцией приведённой толщины проводника при выполнении условия
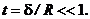
• При малых значениях приведённого радиуса полости погонная токовая индуктивность совпадает со значением 1 нГн/см.
• Погонная потоковая индуктивность любого цилиндрического проводника имеет логарифмическую расходимость при параметре обрезания поля .
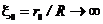• Точное значение параметра обрезания поля и его зависимость от радиуса и длины круглого и трубчатого проводника ожидает своего экспериментального определения.
• Добротность токовой индуктивности цилиндрического проводника не зависит от длины, а зависит от частоты и приведённого радиуса полости.
• Добротность токовой индуктивности имеет приемлемые значения только в некотором частотном диапазоне, ограниченном характеристическими частотами системы.
• С ростом приведённого радиуса полости трубчатого проводника нижняя характеристическая частота увеличивается.
• Увеличение погонной индуктивности цилиндрического проводника при увеличении параметра обрезания поля необходимо учитывать при измерении индуктивности кольцевого тока. Как показывают вычисления в [1], для определённых значений параметра кольца она может быть и значительно меньше индуктивности длинных подводящих проводов.

Статья подготовлена при проведении научных исследований в области фундаментальных основ инженерных наук по проекту, выполняемому в соответствии с соглашением от 21 августа 2012г. № 12-08-00654/12 с федеральным государственным бюджетным учреждением «Российский фонд фундаментальных исследований» на тему «Теоретические основы проектирования интегральных индуктивностей для сложных функциональных блоков и IP-модулей систем связи и телекоммуникаций нового поколения»

Литература:
1. Сапогин, В.Г. Интегральные индуктивности и трансформаторы аналоговых микросхем СВЧ-диапазона. [Текст]: Монография / В.Г. Сапогин, С.Г. Крутчинский, Н.Н. Прокопенко, А.С. Будяков, Е.М. Савченко. - Шахты: ЮРГУЭС, 2010. - 273 с.
2. Матвеев, А.Н. Электричество и магнетизм [Текст]. - М.: Высшая школа, 1983. - 463 с.
3.Манжула, В.Г. Моделирование системного уровня процесса обработки информации при синтезе аналоговых сложных функциональных блоков [Текст] // Системы управления и информационные технологии, 2010. - Т. 41. - № 3. - С. 36-40.
4. Манжула, В.Г. Модели, методы и алгоритмы структурно-параметрического синтеза неизбыточных смешанных СФ-блоков [Текст] // Известия Южного федерального университета. Технические науки, 2011. - Т. 115. - № 2. - С. 79-87.
5. Крутчинский, С.Г. Радиационно-стойкий измерительный усилитель на базе мультидифференциальных входных каскадов [Электронный ресурс] / С.Г. Крутчинский, А.С. Исанин, Н.Н. Прокопенко, В.Г. Манжула // Инженерный вестник Дона, 2012, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2012/1045 (доступ свободный) – Загл. с экрана. – Яз. рус.
6. Манжула, В.Г. Вариативный синтез схемы операционного усилителя с пониженным напряжением смещения нуля [Электронный ресурс/ В.Г. Манжула, И.Б. Пугачев, Н.Н. Прокопенко // Инженерный вестник Дона, 2012, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2012/1037 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Манжула, В.Г. Интерферометрический интерфейс системы определения относительных координат радиоизлучающих объектов [Электронный ресурс/ В.Г. Манжула, С.Г. Крутчинский, А.В. Савенко, В.В. Воронин // Инженерный вестник Дона, 2012, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2012/1027 (доступ свободный) – Загл. с экрана. – Яз. рус.