Математическое моделирование растительных материалов при их соударении с поверхностью
Аннотация
Статья посвящена моделированию соударения растений о неподвижную поверхность. Процесс удара объектов сложной геометрической формы является не до конца изученным. Рассмотрена модель соломистой частицы как ломанного цилиндра.
Ключевые слова: Модель, удар, листостебельный материал, ориентация в пространстве и на плоскости.
При исследовании процессов, связанных с ударными воздействиями на перерабатываемый объект, нужно знать траектории движения компонентов зернового вороха после удара. От анализа этих явлений зависят качественные результаты процессов обмолота и сепарации. Рассмотрим в нецентральный удар частиц вороха о неподвижную поверхность, используя методы классической теории удара [1] – [3].
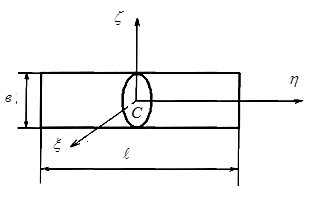
Соломистые частицы представляют собой различные цилиндрические модели. Цилиндр (рис.1) можно описать линзообразной моделью при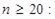 
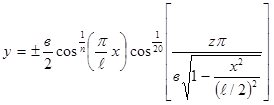(1)
или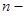 
степенной веретенообразной симметричной моделью с поперечным сечением в виде окружности: 
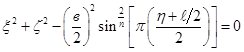(2)
где 
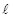и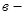 
длина и ширина соломистой частицы. Координаты центра тяжести:
,
,
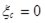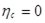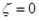. Радиус инерции модели 
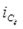. Момент инерции выбранной модели цилиндра можно принять: 
; 
.
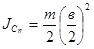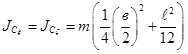Кинематические характеристики равны с учетом того, что Р - точка соприкосновения с неподвижной поверхностью и тело не скользит по ней (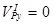
; 
; 
):
, 
, 
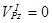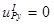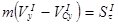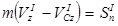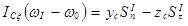; (3)
, 
, 
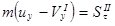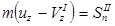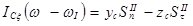; (4)
где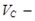 
скорость центра масс зерновки; 
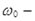угловая скорость зерна, рассмотрим поступательное движение 
; 
, 
,
,
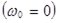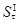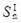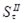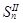- импульсы ударных сил, действующие на тело в первую и вторую фазы удара; 
, 
, 
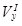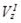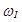- проекции скорости центра масс и угловая скорость в конце первой фазы; 
, 
, 
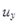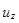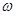- проекции скорости центра масс и угловая скорость в конце второй фазы; 
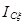- момент инерции выбранной модели зерна относительно подвижной оси
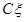, проходящей через центр масс, 
; 
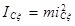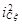- радиус инерции модели; 
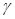- угол падения; ориентация модели определяется углом 
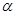между направлением оси модели 
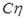и касательной плоскостью к неподвижной поверхности модели. Отношение модулей нормальных составляющих импульсов ударной реакции гладкой поверхности за первую и вторую фазы определяются соотношением 
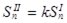, где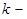 
коэффициент восстановления при ударе соломистой частицы о поверхность.
Параметры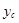 
, 
, 
,
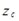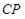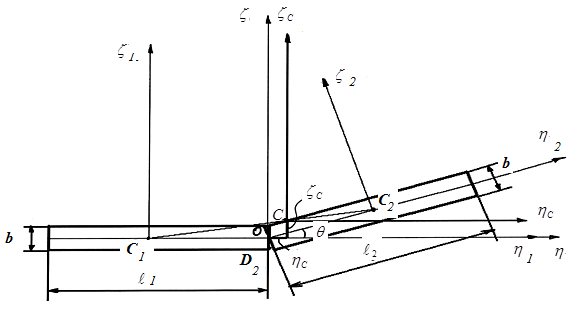
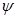равны (рис.2). 
; 
; 
; 
; 
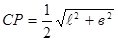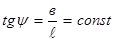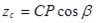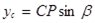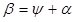. Угол
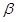и зависит от угла ориентации модели 
; 
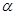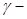угол падения соломистой частицы. В этом случае кинематические характеристики удара не зависят от параметра 
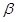. Если ось цилиндра будет искривлена по непрерывной кривой, то этот параметр играет существенную роль и его нужно определять.
Решая систему уравнений (3) – (4) получаем формулы для определения скорости центра масс и угловой в момент окончания, удара угла отражения:
; 
;
;
;
, 
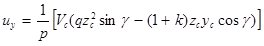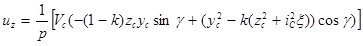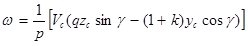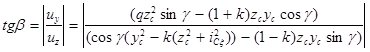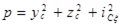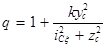. (5)
Рассмотрим еще два случая: модели, состоящие из двух цилиндров, угол между их осями равен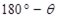 
(рис. 3) и 
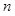– ломаного цилиндра достаточно тонкий, который приближенно описывает криволинейный цилиндр (рис.4). А для n – ломаного цилиндра. Координаты центра тяжести C будут находиться в треугольнике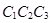 
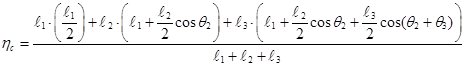
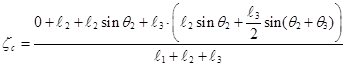(6)
и для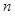 
составляющих получаем
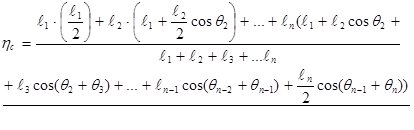
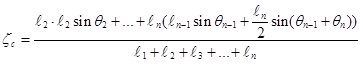(7)
Затем определяем моменты инерции криволинейного цилиндра.
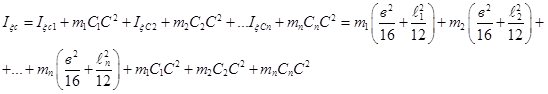(8)
где расстояния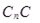 
определяется как расстояние между двумя точкам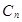и 
и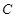 
.
Расстояние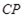 
определяется как расстояние между точкой соприкосновения с поверхностью и центром тяжести. Возьмем ос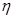и 
и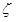 
в точке 
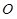. Координаты центра тяжести ломанного цилиндра (рис. 3) равен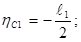 
; 
; 
.
 |
 |
|
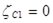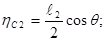
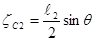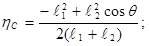
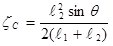Рис. 1. Модель соломистой частицы |
Рис. 3. Расчетная схема для материала, состоящего из двух частей
( ║ ;  ║ ) |
 |
 |
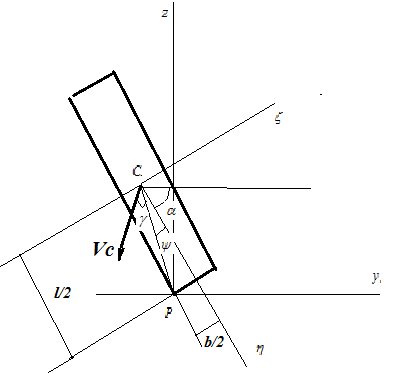
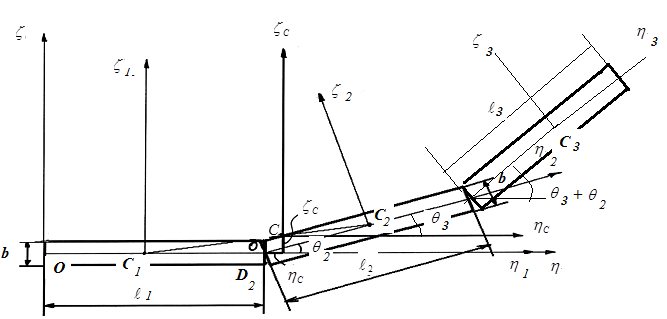
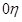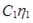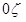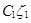| Рис. 2. Расчетная схема соударения соломистой частицы | Рис. 4. Расчетная схема для материала, состоящего из трех частей |
Воспользуемся формулами преобразования моментов инерции каждого цилиндра при параллельном переносе.
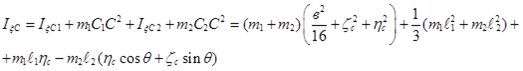(20)
Соударение тела с поверхностью может происходить в точках, для которых расстояния от этих точек до центра тяжести будут равны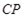 
.
Литература
1. Маяцкая И.А. Основные типы поверхностей моделей семян сельскохозяйственных культур, убираемых зернокомбайнами //Моделирование сельскохозяйственных растительных объектов: Материалы Всероссийского научно-технического семинара 22-24 сентября 1999 г. – Ростов – на – Дону, 2001. – с. 32–35.
2. Маяцкая И.А. К вопросу о соударении семян зерновых культур с поверхностью рабочих органов сельхозмашин. // Разработка технического оснащения производства продукции животноводства. Ст. науч. тр. – Зерноград: ВНИПТИМЭСХ, 2003 г. – с. 199–204.
3. Маяцкая И.А. О построении моделей растительных объектов // Разработка технического оснащения производства продукции животноводства. Ст. науч. тр. – Зерноград: ВНИПТИМЭСХ, 2003 г. – с. 207–213.
Ключевые слова: модель, удар, листостебельный материал, ориентация в пространстве и на плоскости.