Методика численного моделирования спектрометрических газочувствительных сенсорных систем
Аннотация
Рассмотрен принцип функционирования спектрометрических газочувствительных сенсорных систем. Предложены модель и методика численного моделирования спектрометрического газочувствительного сенсора с совмещенным излучателем-приемником инфракрасного излучения на основе перфорированного полупроводникового терморезистора.
Ключевые слова: спектрометрический газочувствительный сенсор, модель, методика моделирования
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Загрязнение атмосферы стало одной из основных проблем современной цивилизации. Выхлопные газы двигателей внутреннего сгорания содержат целый ряд высокотоксичных веществ, таких как окись углерода, углеводороды, окислы азота и др. Концентрации этих веществ в атмосфере неуклонно растут вследствие увеличения числа автомобилей [1]. В результате актуальной задачей является разработка комплексных газоанализаторов, удовлетворяющих современным требованиям по быстродействию и точности, стабильно функционирующих в условиях возмущающих факторов внешней среды. При этом одним из основных этапов разработки газочувствительных сенсорных систем является математическое моделирование, обеспечивающее сокращение сроков и стоимости проектирования сенсорных элементов, а также повышение эффективности проводимых экспериментальных исследований.
Принцип функционирования рассматриваемого в данной работе спектрометрического газочувствительного сенсора схематически представлен на рис. 1 [2].
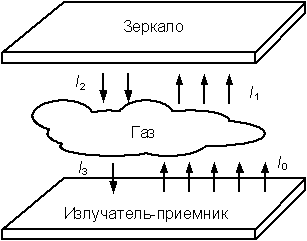
Рисунок 1 - Принцип функционирования спектрометрического газочувствительного сенсора
В качестве излучателя-приемника инфракрасного (ИК) излучения используется полупроводниковый терморезистор. В качестве отражающего зеркала – металлическая крышка корпуса интегральной сенсорной микросистемы. Конструкция корпуса должна обеспечивать доступ атмосферного воздуха в объем между поверхностью микросистемы и внутренней (отражающей) поверхностью крышки (зеркала).
В режиме измерения через полупроводниковый терморезистор пропускается стабильный ток, определяющий температуру поверхности излучателя и, соответственно, интенсивность I0 испускаемого ИК-излучения. Проходя через газ, заполняющий пространство между поверхностями излучателя и зеркала, определенная часть излученной энергии поглощается, причем доля поглощенной энергии зависит от концентрации анализируемого вещества в составе газовой смеси. В результате на поверхность излучателя-приемника будет возвращаться часть потока ИК-излучения интенсивностью I1 < I0, что приводит к изменению температуры и, следовательно, сопротивления излучателя-приемника. При постоянном токе через терморезистор изменение его сопротивления приведет к соответствующему изменению падения напряжения и, как следствие, к изменению интенсивности излучения I0, что приводит к возникновению положительной обратной связи, обеспечивающей повышение чувствительности сенсорной микросистемы. После установления термодинамического равновесия при новом значении концентрации поглощающего вещества в газовой смеси, напряжение на излучателе-приемнике будет определять значение анализируемой концентрации.
Основой сенсора является терморезистор, через который пропускается стабильный ток. Протравленный канал, отделяющий излучатель-приемник от подложки, предусмотрен для увеличения теплового сопротивления терморезистора на подложку. Кроме того, поверхность протравленного канала выполняет роль второго отражающего зеркала, на которое попадает ИК-излучение с нижней поверхности терморезистора, что обеспечивает повышение чувствительности микросенсора.
Повышение селективности микросенсора достигается посредством выполнения перфорации терморезистора отверстиями, диаметр которых соответствует длине волны, на которой наблюдается максимум спектра поглощения анализируемого вещества в составе газовой смеси.
Целью моделирования является определение зависимости напряжения на излучателе-приемнике от концентрации молекул анализируемого вещества в составе газовой смеси с учетом основных параметров микросенсора:
- электрофизических параметров полупроводника;
- геометрических размеров резистора (излучателя-приемника);
- концентрации легирующей примеси в излучателе-приемнике;
- коэффициента поглощения зеркала;
- тока, протекающего через излучатель-приемник.
Основой оптических методов определения концентрации газовых компонент является обобщенный закон Бугера-Ламберта-Бера [3]:
![]() ,(1)
,(1)
где I1 – интенсивность прошедшего через газовую среду излучения; I0– интенсивность излучения источника; kω– показатель поглощения на частоте ω; z – оптический путь или расстояние до источника.
Предполагается, что толщина терморезистора D значительно меньше его длины L и ширины W. При этом площадь боковых поверхностей резистора значительно меньше площади верхней и нижней поверхностей, поэтому с достаточной степенью точности теплопередачей через боковые поверхности в рассматриваемой задаче можно пренебречь.
Принимая во внимание низкую теплопроводность атмосферного воздуха и малые расстояния между поверхностями терморезистора и отражающими зеркалами, теплопередачу посредством конвекции и кондукции с верхней и нижней поверхностей терморезистора можно не учитывать. С учетом принятых допущений, при решении задачи численного моделирования сенсора можно ограничиться двумя пространственными измерениями. Нестационарное распределение температуры во внутренних точках области решения задачи определяется уравнением теплопроводности:
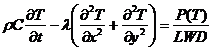 , (2)
, (2)
где x, y – координаты; r – плотность полупроводника; С – удельная теплоемкость полупроводника; T – абсолютная температура; t – время; l – удельная теплопроводность полупроводника; P – мощность, потребляемая терморезистором; L – длина терморезистора; W – ширина терморезистора; D – толщина терморезистора.
В начальный момент времени tmin температура терморезистора определяется температурой подложки T0:
![]() . (3)
. (3)
На границах, соединяющих терморезистор с подложкой, задаются граничные условия первого рода:
![]() ; (4)
; (4)
![]() . (5)
. (5)
С учетом принятых допущений об отсутствии кондукции и конвекции через верхнюю и нижнюю грани терморезистора, теплопередача через данные поверхности происходит посредством излучения и описывается законом Стефана-Больцмана [3]:
![]() (6)
(6)
где с0– коэффициент лучеиспускания абсолютно черного тела; ε – относительная излучательная способность или степень черноты тела; WT – плотность теплового потока.
В соответствии с принципом функционирования микросенсора, законом Бугера-Ламберта-Бера (1) и законом Стефана-Больцмана (6), на верхней и нижней гранях терморезистора задаются граничные условия третьего рода, определяющиеся выражениями:
![]() ; (7)
; (7)
![]() , (8)
, (8)
где RH, RB – коэффициенты отражения верхнего и нижнего зеркал; с – относительное содержание анализируемого компонента в газовой смеси; dH, dB – расстояния от излучающих поверхностей терморезистора до верхнего и нижнего зеркал; a – коэффициент поглощения.
Проводя дискретизацию уравнений (2) – (8) на координатной сетке
![]() (9)
(9)
и сетке по времени
![]() , (10)
, (10)
а также выражая плотность мощности в правой части уравнения (2) через силу тока и удельное сопротивление полупроводника, получим:
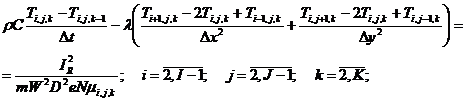 (11)
(11)
![]() . (12)
. (12)
![]() ; (13)
; (13)
![]() . (14)
. (14)
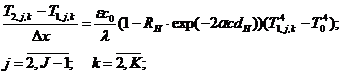 (15)
(15)
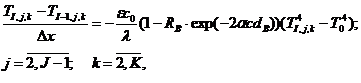 (16)
(16)
где e – элементарный заряд; Δx – шаг координатной сетки по оси x; Δy – шаг координатной сетки по оси y; Δt – шаг сетки по времени; с – относительное содержание анализируемого компонента в газовой смеси; IR – сила тока; N – концентрация легирующей примеси в терморезисторе; m – усредненное отношение площадей поперечного сечения терморезистора с перфорацией и без перфорации; mi,j,k – сеточная функция подвижности носителей заряда; Ti,j,k – сеточная функция температуры.
Дискретная модель (11) – (16) представляет собой систему нелинейных алгебраических уравнений, требующую применения итерационных методов решения. Предложенная методика численного решения состоит в следующем:
10. Ввод исходных данных;
20. Задание требуемого значения невязки ð;
30. Генерация координатной сетки (9) и сетки по времени (10);
40. Определение текущего распределения температуры в терморезисторе в соответствии с начальным условием (12);
50. Нахождение распределения подвижности носителей заряда и правой части уравнения теплопроводности (11);
60. Определение правых частей граничных условий (15), (16);
70. Определение нового приближения к распределению температуры посредством численного решения системы алгебраических уравнений (11) – (16), которая с учетом определенных в пп. 50 и 60 правых частей уравнений (11), (15), (16) становится линейной;
80. Определение невязки в соответствии с выражением:
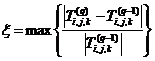 , (17)
, (17)
где q – порядковый номер итерации;
90. Если выполняется неравенство ξ > d, найденное нестационарное распределение температуры считается текущим и осуществляется переход к п. 50, в противном случае – переход к п. 100;
100. Повторение пп. 40 – 90 для всех исследуемых значений относительного содержания анализируемого компонента в газовой смеси;
110. Определение и вывод зависимости изменения напряжения на терморезисторе от относительного содержания анализируемого компонента в газовой смеси, определение чувствительности, времени установления в рабочий режим и времени отклика микросенсора.
Разработанные модель и методика численного моделирования позволяют проводить детальный анализ влияния различных параметров газочувствительного микросенсора на его выходные характеристики, что дает возможность рассматривать предложенные модель и методику в качестве основы для соответствующих систем автоматизированного проектирования газочувствительных спектрометрических микросистем.
Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.А18.21.2052 «Разработка технологии формирования наноструктурированных материалов и гибридных сенсорных систем на их основе».
Литература:
- Д.О. Горелик; Л.А. Конопелько. Мониторинг загрязнения атмосферы и источников выбросов: Аэроаналитические измерения. – М.: Изд-во стандартов, 1992. – 432с.
- Дж. Фрайден. Современные датчики. Справочник.– М.: Техносфера, 2005. – 592 с.
- Х.Кухлинг. Справочник по физике. – М.: Мир, 1982. – 520 с.