Моделирование напряженного состояния арматурных стержней, применяемых при производстве преднапряженных железобетонных конструкций

О.А. Бурцева; Е.Е.Косенко; В.В. Косенко; В.В.Нефедов; А.В.Черпаков

Моделирование напряженного состояния арматурных стержней, применяемых при производстве преднапряженных железобетонных конструкций

Аннотация

О.А. Бурцева, Е.Е.Косенко, В.В. Косенко, В.В.Нефедов, А.В.Черпаков

В статье представлены результаты моделирования напряженного состояния арматурного стержня из стали класса Ат800 без внешних концентраторов напряжений. Определяется уровень допустимого упрочнения одноосным растяжением арматуры, исходя из условия появления предельных напряжений в сечении образцов арматурных сталей.
Ключевые слова: арматура, моделирование напряженного состояния, арматурный стержень, коэффициент упрочнения.

05.23.05 - Строительные материалы и изделия

05.23.17 - Строительная механика

При изготовлении железобетонных конструкций в настоящее время эффективно используются современные виды арматурных сталей изготовленных способом термомеханического упрочнения [1, 2]. С помощью этого способа изготовления в арматуру закладывают значительный прочностной потенциал, обеспечивая требуемые пластические свойства. Такое сочетание свойств обеспечивает сложная структура в сечении арматуры, изменяющаяся от бейнитной с различным соотношением отпущенного мартенсита, цементита и остаточного аустенита в поверхностном слое до феррито-перлитной в сердцевине. Полученная неоднородная структура имеет различные механические характеристики, которые позволяют упрочнять арматуру одноосным растяжением [3, 4]. Подобный вид воздействия приводит к некоторому снижению пластичности, и как следствие, к упрочнению материала арматуры.
Ранее проведенными исследованиями [3, 4] установлена возможность упрочнения одноосным растяжением арматуры класса Ат800 до коэффициента упрочнения = 1,15 . Коэффициент упрочнения К_у представляет собой отношение действующего напряжения к физическому или условному пределу текучести. В процессе изготовления у таких видов арматуры наряду со сложной структурой сечения [2] создается сложный рельеф поверхности, характеризующийся наличием концентраторов напряжений, в виде периодического профиля и соответственно различными отклонениями значений диаметра. Упрочнение арматуры выше значений предела текучести вызывает увеличение напряжений в сечении, при этом в поверхностном слое эти изменения больше, в отличие от сердцевины [3]. При исследовании влияния упругопластического деформирования на свойства материала арматуры, наряду с концентраторами напряжений необходимо учитывать отклонения диаметра, т. к. при упрочнении одноосным растяжением арматуры длиной 6 и более метров (например, до коэффициента упрочнения = 1,05.), наибольшие напряжения, очевидно, будут возникать в местах с наименьшей площадью сечения, при этом их значения в различных зонах могут превышать номинальное. Механические характеристики в сечении арматуры были получены с помощью неразрушающего метода, основанного на ударном вдавливании усеченного индентора [5, 6].
Цель работы. Анализ напряженно-деформированного состояния арматурной стали класса Ат800 при нагрузках превышающих значение предела текучести. Определение уровня допустимого упрочнения одноосным растяжением арматуры, исходя из условия появления предельных напряжений в сечении образцов арматурных сталей.
Моделирование напряженного состояния. С помощью конечно-элементного комплекса ANSYS была построена плоская модель стержня на основе конечного элемента PLANE42. Диаметр арматурного стержня D=12.2мм. Длина стержня L=100 мм. В задаче не рассматривается влияние внешних концентраторов напряжений, в следствии чего, в данной модели отсутствует внешний периодический профиль. Разбивка моделей на узлы по длине производилась кратной 1/80 от общей длины и кратной 1/20 основания (радиуса) стержня. Количество конечных элементов - более 1600. Поскольку задача является симметричной, то имеет смысл для решения рассматривать только 1/2 часть всей модели, что существенно сокращает количество элементов в сетке. При этом реальное усилие, действующее на образец, будет в 2 раза больше заданного.

Рис. 1. Граничные условия для решения задачи

Модельный образец по радиусу сечения делится на семь равных по величине зон, для которых задаются соответствующие механические характеристики. Для моделирования упругопластических свойств стержня применяли мультилинейную модель с использованием схемы диаграммы напряжение – деформация (σ-ε). Механические характеристики стержня в зоне упругости задаем упругими константами – модулем упругости E = 2,05×1011 Па и коэффициентом Пуассона μ = 0,3, а в зоне пластики - кусочно-линейной зависимостью s(e) [7, 8]. Распределение механических характеристик по слоям представлено в таблице 1, а графическое отображение – на рис. 2.
Поверхностный слой характеризуется значением предела текучести 1046 МПа, в сердцевине он составляет 963 МПа. Значения предела прочности приняты равными в поверхностном слое 1342 МПа, в сердцевине - 1016 МПа.
Нагрузка P к стержню прикладывалась в направлении оси OZ смещением верхних узлов.
Задавались следующие граничные условия (рис. 1):

- все точки упругопластической области с координатой z=0 закреплены в вертикальном направлении (U_z=0);

- все точки, лежащие на оси симметрии закреплены в радиальном направлении (U_r=0);

- нагрузку на образец моделировали последовательным смещением верхних узлов, величина которой составляет 1,05 и 1,15 sт.

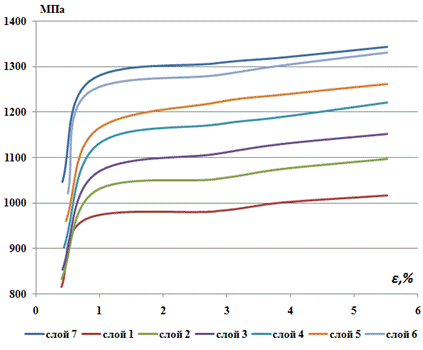
Рис. 2. Графическое отображение распределения зависимостей σ-ε для каждого из слоев

Таблица 1
Задание механических свойств для мультилинейной модели зависимостей σ-ε для соответствующих слоев

№ слоя	свойства	Точки для задания свойств зависимости *σ-ε*
№ слоя	свойства	1	2	3	4	5
1	ε, %	0,3974	0,783	2,82	3,87	5,51
1	σ, МПа	814,8	963,7	981,0	1000,0	1016,0
2	ε, %	0,4057	0, 934	2,82	3,87	5,51
2	σ, МПа	831,7	1025,6	1052,2	1074,2	1096,1
3	ε, %	0,4158	0,934	2,82	3,87	5,51
3	σ, МПа	852,5	1063,4	1106,6	1128,8	1150,9
4	ε, %	0,4394	0,961	2,82	3,87	5,51
4	σ, МПа	900,8	1128,1	1172,2	1188,4	1220,2
5	ε, %	0,4683	0,951	2,82	3,87	5,51
5	σ, МПа	960,1	1160,3	1220,4	1238,0	1260,6
6	ε, %	0,498	0,81	2,82	3,87	5,51
6	σ, МПа	1021,0	1240,3	1280,7	1302,2	1330,1
7	ε, %	0,4104	0,84	2,82	3,87	5,51
7	σ, МПа	1046,5	1268,3	1307,0	1320,1	1343,0

Результаты решения статической задачи представлены на рис. 3 - 5 в виде полей напряжений образца. На рис. 3 отчетливо видны значения напряжений в сечении арматурного стержня в момент приложения нагрузки, из чего можно сделать вывод, что приложение нагрузки,

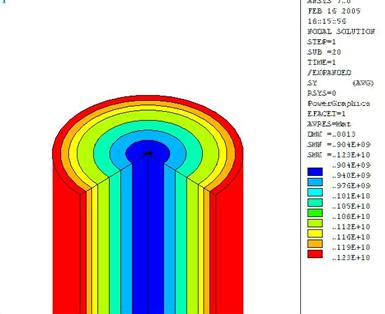
Рис. 3. Значения напряжений в эквивалентном сечении стержня в момент приложения нагрузки, соответствующей Ку = 1,05
(ε = 0,84)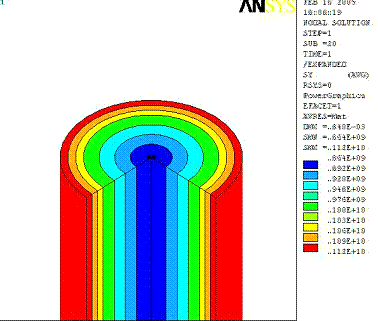

Рис. 4. Значения напряжений в эквивалентном сечении стержня в момент приложения нагрузки, соответствующей Ку = 1,15
(ε = 1,28%)

соответствующей = 1,05 , приводит к появлению напряжения по сечению стержня, составляющего в поверхностном слое 1120 МПа и соответствующего коэффициенту упрочнения = 1,07 , а в сердцевине - 864 МПа, что соответствует = 1,05 . Полученные коэффициенты упрочнения незначительно отличаются от значений приложенной нагрузки. Однако увеличение общей нагрузи до напряжений соответствующих = 1,15 приводит к увеличению напряжений в поверхностном слое до 1280 МПа, что составляет = 1,22 (рис. 4), в сердцевине - до 904 МПа ( = 1,1 ). Уровень напряжений в поверхностном слое превышает допустимый, принятый в настоящей работе = 1,15 .
Для наглядности на рис. 5 показаны зависимости напряжений в сечении стержня от коэффициента упрочнения. Из графиков видно, что при увеличении нагрузки в поверхностном слое напряжения, соответствующие коэффициенту большей пластичностью сердцевины и меньшим значением предела текучести. На рис. 6 представлены расчетная и экспериментальная диаграммы. Ошибка составляет около 2 %, что подтверждает достоверность проведенных расчетов.
Выводы. Полученные значения допустимых коэффициентов упрочнения для исследуемых классов арматуры несколько снижают полученные ранее значения предельных напряжений. Проведенные расчеты позволяют говорить о возможности использования полученных данных для упрочнения стержней арматурных сталей.
Работа выполнена при частичной поддержки РФФИ (грант №11-08-90728 моб_ст, 11-08-90726 моб_ст)

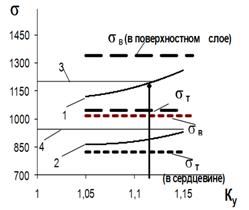
Рис. 5. Изменение напряжений в эквивалентном сечении арматуры класса Ат800 в зависимости от коэффициента упрочнения: 1 – в поверхностном слое; 2 – в сердцевине; 3, 4 – уровень напряжений, соответствующих = 1,15 .

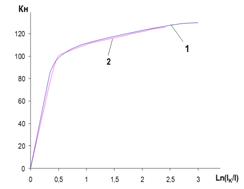
Рис. 6. Диаграммы растяжения арматуры класса Ат800:
1 – экспериментальная; 2 - расчетная

Моделирование напряженного состояния арматурных стержней, применяемых при производстве преднапряженных железобетонных конструкций

Литература.