Моделирование параметров МОП-транзисторов в широком температурном диапазоне

Аннотация

А.М. Пилипенко, В.Н. Бирюков

Дата поступления статьи: 26.11.2013

Измерены зависимости от температуры основных параметров моделей p-канальных МОП-транзисторов в широком диапазоне температур – от криогенных до комнатных (20 … 300 К). Предложена универсальная формальная четырехпараметрическая модель, позволяющая аппроксимировать все измеренные в работе температурные зависимости параметров с относительной погрешностью не более 1 %. Модель предназначена для МОП-транзисторов, применяющихся в малошумящих усилителях радиоприемных устройств оптического и инфракрасного диапазона на астрономических спутниках, радиотелескопах и космических обсерваториях. Полученные результаты могут быть использованы для моделирования температурных режимов усилителей на МОП-транзисторах в электронных симуляторах SPICE-типа. 

Ключевые слова: МОП-транзистор, параметры МОП-транзистора, криогенные температуры, измерение параметров, температурные зависимости

05.13.18 - Математическое моделирование, численные методы и комплексы программ

05.27.01 - Твердотельная электроника, радиоэлектронные компоненты, микро- и наноэлектроника на квантовых эффектах

В настоящее время для реализации избирательных усилителей в системах на кристалле широко используются МОП-транзисторы, которые позволяют расширить диапазон рабочих частот усилителей и существенно упростить согласование их звеньев [1]. Для улучшения основных характеристик МОП-транзисторов и повышения их надежности усилительные устройства часто работают при низких (криогенных) температурах. Охлаждение устройства позволяет увеличить крутизну МОП-транзистора и уменьшить собственные шумы [2]. Последнее особенно важно для малошумящих усилителей, которые используются в радиоприемных устройствах оптического и инфракрасного диапазона на астрономических спутниках, радиотелескопах и космических обсерваториях [3, 4]. Охлаждение до температур меньше 100 К может быть достигнуто при помещении усилителя в криогенные жидкости, полученные при ожижении газов (кислорода, азота, неона, водорода или гелия) [5].
Основными достоинствами МОП-транзисторов перед другими типами транзисторов являются наиболее развитая технология серийного производства, широкое коммерческое использование и низкая стоимость. К недостаткам МОП-транзисторов можно отнести аномальное поведение вольт-амперных характеристик (ВАХ) n-канальных МОП-транзисторов («гистерезис» и «kink-эффект»), которое наблюдается при температурах ниже 40 К [4].
Аналитические выражения для температурных зависимостей параметров МОП-транзисторов известны только для комнатных и высоких температур (290 … 420 К) [6, 7]. Для низких температур разработан ряд моделей, позволяющих описать статические и дифференциальные характеристики МОП-транзисторов [8, 9]. Целью настоящей работы является измерение и аппроксимация температурных зависимостей основных параметров моделей p-канальных МОП-транзисторов в широком диапазоне температур – от криогенных до комнатных (20 … 300 К). Указанные зависимости предназначены для моделирования температурных режимов усилителей на МОП-транзисторах в электронных симуляторах SPICE-типа. Решение данной задачи позволит прогнозировать время работоспособности устройства при изменении температуры в случаях аварийных или внештатных ситуаций, а также оптимизировать выбора хладагента и повысить надежность усилителя в условиях криогенных температур.
Описание МОП-транзисторов и их модели
В данной работе проведено измерение параметров моделей для ряда температур и получены зависимости параметров от температуры для двух тестовых образцов p-канальных МОП-транзисторов с поликремниевым затвором. Первый транзистор с размерами W ≈ 50 мкм и L ≈ 50 мкм (W / L = 50/50), где Wи L– ширина и длина канала соответственно был изготовлен специально для целей измерения параметров. Второй транзистор с размерами W ≈ 10 мкм и L ≈ 6 мкм (W / L = 10/6) соответствовал транзисторам усилительного устройства. Выбор сравнительно большой длины канала объясняется необходимостью снижения собственных шумов транзисторов.
В работе [9] показано, что для достаточно точного описания статических ВАХ МОП-транзистора при низких температурах можно использовать компактную пятипараметрическую модель, которая имеет следующий вид
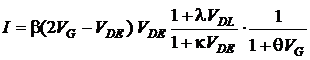  (1)                     
где I – ток стока; VGS, VDS – напряжения затвор-исток и сток-исток соответственно; VG = VGS – VT0 – напряжение отсечки;  –напряжение насыщения; ; ;  мВ и  – формальные константы;β, VT0, λ, k, θ – параметры модели.
Все параметры модели (1) являются физическими: β – удельная крутизна; VT₀ – пороговое напряжение; λ – коэффициент модуляции длины канала напряжением стока; k– параметр, учитывающий снижение подвижности носителей заряда в продольном электрическом поле канала;θ–параметр учитывающий влияние поперечного поля на подвижность носителей заряда. Следует отметить, что для повышения точности моделирования ВАХ, вместо модели (1) можно использовать таблично-аналитическую модель, описанную в работе [10] и имеющую те же физические параметры.
Методика измерения параметров модели
Основными параметрами модели МОП-транзистора являются удельная крутизна, пороговое напряжение и коэффициент модуляции длины канала – β, VT₀ и λ [9]. Параметры, учитывающие зависимость подвижности носителей заряда от величины поперечной и продольной составляющих электрического поля существенно влияют на точность модели, но являются плохо обусловленными (их величина наиболее сильно зависит от выбранной для измерения области ВАХ и числа измерений) [11]. Классификация параметров необходима для организации их измерений. Если все параметры определять одновременно, то оптимизация целевой функции в методе наименьших квадратов при различных температурах приводит к значительному хаотическому изменению параметров. Для повышения обусловленности параметрической идентификации вспомогательные параметры определялись приближенно на образцах транзисторов с размерами W ≈ 50 мкм и L ≈ 50 мкм и далее считались заданными. Падение точности моделирования оказывается при этом несущественным, а процедура численной оптимизации значительно упрощается за счет снижения размерности задачи.
Численные эксперименты показали, что для получения наибольшей точности моделирования ВАХ исследуемых в данной работе МОП-транзисторов следует положить k = 0,02 В ^– 1, θ = 0,1 В ^– 1. В качестве целевой функции использовалась сумма квадратов относительных погрешностей моделирования тока
,
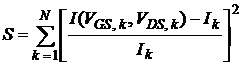где {I k , V_GS, k , V_DS, k},  k = 1, 2, ..., N – экспериментальная ВАХ МОП-транзистора в табличной форме, N – количество точек ВАХ.
Следует отметить, что параметр λ определяет наклон пологого участка выходных ВАХ и не имеет физического смысла на крутом участке, поэтому для его идентификации использовались только те точки экспериментальной ВАХ, которые лежат на пологом участке. При W / L = 50/50 значение λ оказалось значительно меньше единицы (λ ≈ 10 ^- 4 …10 ^- 3 В^-1), поэтому зависимость λ(T) в этом случае достоверно измерить не удалось. При W / L = 10/6, как показано ниже, значение λ значительно больше, чем 10 ^– 3 В^–1 и зависит от температуры.
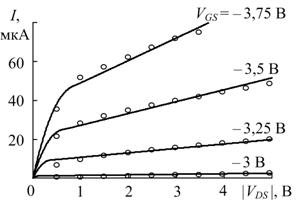
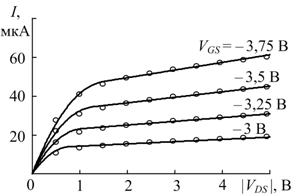
ВАХ исследуемых МОП-транзисторов измерялись при пяти температурах – 20, 40, 80, 160 и 300 К. На рис. 1 приведены экспериментальные (прямоугольники) и расчетные (линии) ВАХМОП-транзистора с размерами W ≈ 50 мкм и L ≈ 50 мкм при температурах 20 и 300 К, а на рис. 2 приведены аналогичные ВАХ МОП-транзистора с размерами W ≈ 10 мкм и L ≈ 6 мкм. Во всех случаях определялись среднеквадратические погрешности моделирования ВАХ : при W / L = 50/50 -  %, при W / L = 10/6 -  %.

       
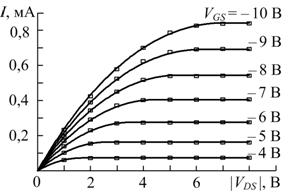
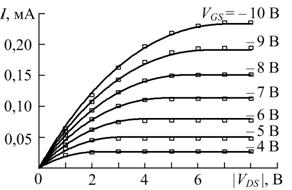
а)                                                               б)
Рис. 1. – Расчетные и экспериментальные ВАХМОП-транзистора
с размерами W ≈ 50 мкм и L ≈ 50 мкм при T = 20 К (а) и 300 К (б)

   
а)                                                               б)
Рис. 2. – Расчетные и экспериментальные ВАХМОП-транзистора
с размерами W ≈ 10 мкм и L ≈ 6 мкм при T = 20 К (а) и 300 К (б)

Аппроксимация температурных зависимостей параметров модели

Температурные зависимости параметров моделей аппроксимируются или физически или формально. Разработка физической температурной модели крайне трудоемка и такая модель требует постоянной проверки и корректировки при изменении технологического процесса изготовления транзисторов. Формальная аппроксимация максимально оперативна и максимально достоверна. В настоящей работе использована аппроксимация зависимостей основных параметров модели МОП-транзистора от температуры дробно-рациональной функцией
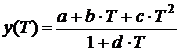,   (2)                                   
где a, b, c, d – параметры аппроксимации.
Относительная погрешность аппроксимации при температуре T_i имеет вид
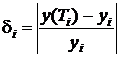, (3)                                       
где y(T_i) – значение параметра МОП-транзистора, полученное с помощью функции (2); y_i – измеренное значение параметра МОП-транзистора при температуре T_i.
Вид аппроксимирующей функции выбран таким образом, чтобы при использовании метода наименьших квадратов задача параметрической оптимизации всегда имела единственное решение, – три из четырех параметров входят в выражение (2) линейно, то есть задача численного спуска сводится к одномерной (аналогичный прием использован в [11]). На рис. 3 представлены измеренные зависимости параметров МОП-транзисторов от температуры и функции, аппроксимирующие эти зависимости (сплошные линии), кривая 1 соответствует W / L = 10/6, кривая 2 –W / L = 50/50.

  
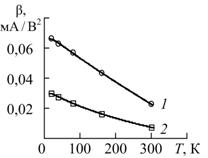
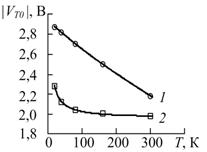
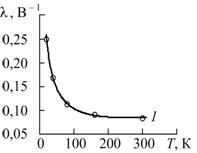
а)                                        б)                                  в)
Рис. 3. – Зависимости параметров b, |VT0| и λ от температуры
при W / L = 10/6 (кривая 1) и W / L= 50/50 (кривая 2)

В рассмотренных выше примерах задача оптимизации оказалась очень хорошо обусловленной, что позволило получить параметры аппроксимации не только в среднеквадратическом, но и в равномерном приближении. Такой подход позволяет минимизировать максимальную относительную погрешность аппроксимации и одновременно получить ее апостериорную оценку. На рис. 4 показаны вычисленные по формуле (3) зависимости от температуры относительных погрешностей аппроксимации параметров МОП-транзистора с размерами W ≈ 10 мкм и L ≈ 6 мкм, кривая 1 соответствует параметру b, кривая 2 - |VT₀|, кривая 3 - λ.

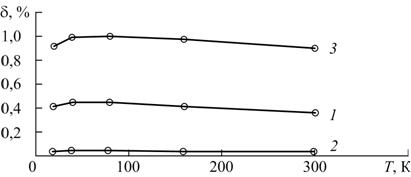
Рис. 4. – Зависимости от температуры относительных погрешностей аппроксимации параметров b (кривая 1), |VT₀| (кривая 2) и λ (кривая 3)

Из результатов, приведенных на рис. 4 следует, что максимальная относительная погрешность аппроксимации температурных зависимостей параметров МОП-транзистора с помощью формальной модели (2) не превышает 1 %. Погрешность аппроксимации не растет на краях интервала наблюдения, что позволяет при необходимости увеличить его без замены аппроксимирующей функции.

Выводы

В работе получены экспериментальные зависимости основных параметров МОП-транзистора от температуры в широком диапазоне температур – от 20 до 300 К. Предложена модель в виде дробно-рациональной функции, позволяющая с высокой точностью аппроксимировать все измеренные температурные зависимости. При использовании предложенной аппроксимирующей функции ошибка определения параметров МОП-транзистора может быть получена существенно меньше разброса параметров в технологическом процессе.

Работа выполнена при поддержке стипендии Президента Российской Федерации молодым ученым и аспирантам, осуществляющим перспективные научные исследования по приоритетным направлениям модернизации российской экономики (СП-398.2012.5).

Литература:

1. Жебрун Е.А., Миляева С.И., Прокопенко Н.Н. Высокочастотные избирательные усилители и полосовые фильтры на КМОП транзисторах SiGe техпроцесса [Электронный ресурс] // Инженерный вестник Дона, 2012, № 3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/1033 (доступ свободный) – Загл. с экрана. – Яз. рус.
2. Бирюков В.Н., Пономарев А.М., Ципис Н.Л. Исследование вольтам­перных и шумовых характеристик полевых транзисторов с изолированным затвором при низких температурах // Известия вузов МВ и ССО СССР. Радиоэлектроника, 1986, Т. 29, № 11. – С. 92-94
3. Fanson J. L., Fazio G. G., Houck J. R., Kelly T., Rieke G. H., Tenerelli D. J., Whitten T. Space infrared telescope facility (SIRTF) // Proceedings of SPIE, 1998, V. 3354. – P. 57-65.
4. Nagata H., Shibai H., Hirao T., Watabe T., Noda M., Hibi Y., Kawada M., Nakagawa T. Cryogenic Capacitive Transimpedance Amplifier for Astronomical Infrared Detectors // IEEE Transactions on Electron Devices, 2004, V. 51, N. 2. – P. 270-278.
5. Алфеев В.Н. Полупроводники, сверхпроводники и параэлектрики в криоэлектронике: свойства и применение в криоэлектронных интегральных схемах и приборах структур на основе контактов полупроводников, сверхпроводников и параэлектриков [Текст]. – М.: Сов. радио, 1979. – 408 с.
6. Cheng Y., Imai K., Jeng M., Liu Z., Kai C., Hu C. Modelling temperature effects of quarter micrometre MOSFETs in BSIM3v3 for circuit simulation // Semiconductor Science and Technology, 1997, V. 12, No. 11. – P. 1349-1354.
7. HSPICE® Reference Manual: MOSFET Models. Version D-2010.12 – Synopsys, Inc., 2010. – 768 p.
8. Kan J., Weifeng S., Longxing S. A sub-circuit MOSFET model with a wide temperature range including cryogenic temperature // Journal of Semiconductors, V. 32, N. 6. – Available at: http://dx.doi.org/10.1088/1674-4926/32/6/064002.
9. Пилипенко А.М. Бирюков В.Н. Исследование параметров полевых транзисторов с изолированным затвором при низких температурах [Текст] // Успехи современной радиоэлектроники, 2011, № 9. – С. 66-70.
10. Бирюков В.Н., Пилипенко А.М., Семерник И.В. Таблично-аналитическая модель полевого транзистора для криогенных температур [Электронный ресурс] // Инженерный вестник Дона, 2012, № 4, Ч. 2. – Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1402 (доступ свободный) – Загл. с экрана. – Яз. рус.
11. Бирюков В.Н. Оценка точности определения параметров моделей полевого транзистора [Текст] // Известия вузов. Электроника, 2010, № 5. – С. 39-44.