Итерационный алгоритм оптимального управления компенсационными преобразователями
Аннотация
Дата поступления статьи: 17.10.2013Предложен алгоритм управления компенсационными преобразователями, обеспечивающий управление активной и реактивной составляющих потребляемой мощности. Алгоритм позволяет найти оптимальное соотношение между значениями углов управления αе и αи. В используемом алгоритме лежит способ решения уравнений при помощи итераций .В статье использованы материалы госконтракта № 16.526.12.6016 от 11.10.2011.
Ключевые слова: компенсационный преобразователь, двухзвенный преобразователь частоты, алгоритм управления, целевая функция, итерационный метод
05.13.05 - Элементы и устройства вычислительной техники и систем управления
Авторы рассматривают вопрос реализации алгоритма оптимального управления активным компенсационным выпрямителем[1] (АКВ) с раздельным управлением вентилями катодной и анодной групп. Схема АКВ в составе двухзвенного преобразователя частоты [2, 3] приведена на рис.1. Для формирования необходимого значения выпрямленного напряжения и величины потребляемой, либо генерируемой в сеть, реактивной мощности, требуется вычислитьпрограммные (задающие) значения углов управления групп вентилей
и 
[4]. Произведем такие вычисления при общепринятых допущениях о значительной индуктивности в цепи постоянного тока.
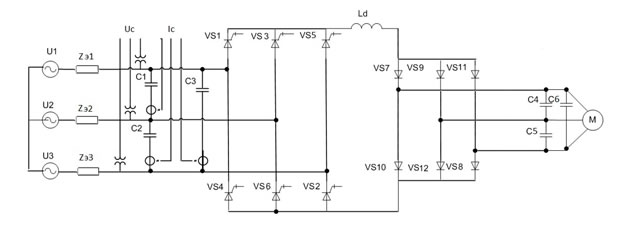
Рис. 1. - Принципиальная схема двухзвенного преобразователя частоты с компенсационным преобразователем
Значения мощности искажения, активной и реактивной мощности зависят от углов управления и [5].
,
,
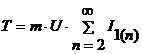
где 
- количество фаз преобразователя;
- сдвиг фаз между первыми гармониками питающего напряжения и тока.
Задача управления компенсационным выпрямителем - поиск соотношения между значениями управляющих углов и , которые обеспечат минимум целевой функции:
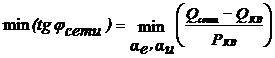, (1)
где 
- реактивная мощность компенсационного выпрямителя;
- активная мощность компенсационного выпрямителя;
- требуемая реактивная мощность для распределительной сети.
Эту задачу решает устройство оптимизации, включенное в состав системы управления компенсационным выпрямителем.
Во время работы, компенсационный выпрямитель должен решать две основных задачи. Во-первых, требуется обеспечить технологический процесс за счет активной мощности
, получаемой с выхода АКВ. При этом напряжение на выходе АКВ определяется следующей формулой:
.
Во-вторых, необходимо генерировать в сеть реактивную мощность емкостного характера:
,
де
и
.
При решении задач оптимизации будем рассматривать необходимый установившийся режим (процесс) на выходе компенсационного выпрямителя, при котором I=const, U=const, т.е. режим, характеризующийся параметром
.
При этом справедливо соотношение: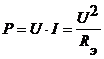
Получаем функционально-технологическое ограничение в системе электроприемника постоянного тока:
.
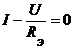Составим функцию Лагранжа:
Необходимо найти и приравнять к нулю выражения
,
, 
, они систему уравнений, решение которых - 
, 
, 
– обеспечит минимум функции (1).
Таким образом, для первого уравнения имеем: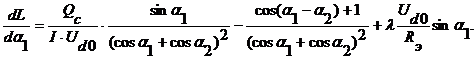
Для 2-го уравнения: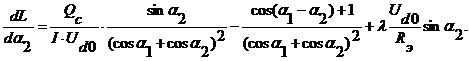
В итоге, получим систему уравнений для нахождения значений
, 
, 
:
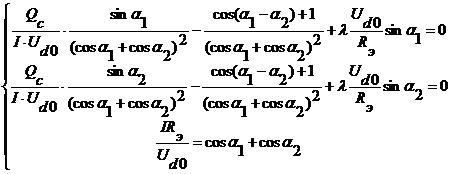(2)
В используемом алгоритме применен способ решения уравнений при помощи итераций [6, 7], реализующий достижение условия:
.
После интегрированияпроизводной неизвестной (искомой) переменной, её текущие значения «х» подставляются в выражение
, формирующее штрафную функцию:
.
На рис. 2 показана вычислительная схема, лежащая в основе оптимизирующего устройства в системе управления преобразователем, обеспечивающая решение системы уравнений (2).
Рис. 2. - Вычислительная схема решения нелинейных и нестационарных уравнений
При моделировании нелинейной схемы вычисления углов управления использован метод Эйлера [8, 9]:
.
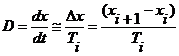Решение указанных в данном разделе задач возможно при использовании микропроцессорных средств.В качестве базы для реализации комплексной системы управления могут использоваться сигнальные процессоры[10].
Литература:
1. Зайцев А.И. Применение компенсационных преобразователей в целях энергосбережения / А.И. Зайцев, А.С. Плехов // Электротехнические комплексы и системы управления. Воронеж, 2010. №4(20).с.38-44.
2. Чивенков, А.И. Расширение функциональных возможностей инвертора напряжения систем интеграции возобновляемых источников энергии и промышленной сети [Электронный ресурс] / А.И. Чивенков, В.И. Гребенщиков, А.П. Антропов, Е.А. Михайличенко // «Инженерный вестник Дона», 2013. №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2013/1564 (доступ свободный) – Загл. с экрана. – Яз. Рус.
3. Кондратьева Н.П. Инновационные энергосберегающие электроустановки для предприятий АПК Удмуртской Республики. [Электронный ресурс] / Н.П.Кондратьева, С.И.Юран, И.Р.Владыкин, Е.А. Козырева, И.В.Решетникова, В.А.Баженов, В.М.Литвинова //«Инженерный вестник Дона», 2013. №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2013/1632 (доступ свободный) – Загл. с экрана. – Яз. Рус.
4. Generalized Predictive Direct Power Control for AC/DC Converters/ Ricardo P. Aguilera, Daneil E. Quevedo// ECCE Asia Downunder (ECCE Asia), 2013 pp 1215-1220.
5. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты // Екатеринбург: УРО РАН, 2000. 654 с.
6. Плехов А.С. Задачи идентификации и оптимизации при энергосберегающем управлении электроприводами и алгоритмы их решения / А.С. Плехов, М.Н. Охотников, В.Г. Титов // Труды Нижегородского государственного технического университета им. Р.Е. Алексеева. НижнийНовгород, 2011, № 3(90), с. 215-225.
7. Kelley, C.T. Iterative methods for optimization / C. T. Kelley // Society for Industrial and Applied Mathematics, 1999 – 196 p.
8. Солонина А.И. Основы цифровой обработки сигналов. Курс лекций. / Солонина А.И., Улахович Д.А., Арбузов С.М., Соловьева Е.Б.// Изд. 2-е испр. и перераб. – Спб.: БХВ – Петербург, 2005. – 768 с.
9. Бабенко К.И. Основы численного анализа. – Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2002. – 848 с.
10. Сперанский В.С. Сигнальные микропроцессоры и их применение в системах телекоммуникаций и электроники. Учебное пособие для вузов. – М.: Горячая линия – Телеком, 2008. – 168 с.