Колебания многослойной полуплоскости с относительно сильно заглубленной полостью произвольной формы
Аннотация
Дата поступления статьи: 18.11.2013Рассмотрено решение задачи о колебания многослойной полуплоскости с полостью произвольной формы методом граничных интегральных уравнений. Для случая относительно сильного заглубления полости использованы асимптотическое представление фундаментальных решений. Приведены результаты решения задачи для перемещений и напряжений вблизи поверхности полости методом граничных элементов.
Ключевые слова: многослойная среда, полость произвольной формы, асимптотический анализ, метод граничных интегральных уравнений
При проектировании строительных объектов в сейсмоопасных регионах необходимо учитывать строение и свойства основания, как правило, многослойного, а также наличие возможных заглубленных в него неоднородностей типа полостей или включений. Сложности математического моделирования динамических процессов в таких областях обусловлены большим числом параметров задачи и наличием отражающих и преломляющих поверхностей различной формы (плоские и криволинейные поверхности). В случае, когда полость имеет каноническую форму (круговой или эллиптический цилиндр, сфера), развиты подходы сведением краевой задачи к системе линейных алгебраических уравнений [1,2], а также использованием асимптотических методов [3,4]. При существенном отличии формы полости или включения от канонической наиболее распространенным является использование метода граничных интегральных уравнений (ГИУ) [5,6]. При большом количестве слоев основания решение систем ГИУ представляет достаточно серьезную проблему. По этой причине в случае, когда полость произвольной формы достаточно сильно удалена от дневной поверхности представляется целесообразным использовать асимптотические методы для упрощения решении систем ГИУ.
Рассматривается упругая ![]() - слойная полуплоскость, занимающая в декартовой системе координат
- слойная полуплоскость, занимающая в декартовой системе координат ![]() область
область ![]() , как показано на рис. 1. Полуплоскость содержит заглубленную неоднородность с замкнутой кусочно-гладкой границей
, как показано на рис. 1. Полуплоскость содержит заглубленную неоднородность с замкнутой кусочно-гладкой границей ![]() . Колебания в установившемся гармоническом с частотой
. Колебания в установившемся гармоническом с частотой ![]() режиме возбуждаются заданным на границе полости вектором распределенных усилий
режиме возбуждаются заданным на границе полости вектором распределенных усилий ![]() , а на дневной поверхности среды в ограниченной области
, а на дневной поверхности среды в ограниченной области ![]() – вектором напряжений
– вектором напряжений ![]() (рис.1).
(рис.1).
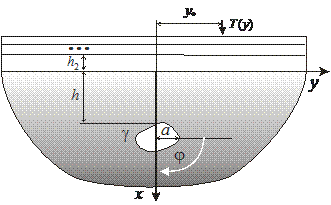
Рис. 1
Рассматривается случай относительно сильно заглубленной полости при наложении ограничения
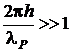 , (1)
, (1)
здесь ![]() - минимальное расстояние между границами полуплоскости и полости,
- минимальное расстояние между границами полуплоскости и полости, ![]() - длина продольной волны в полуплоскости.
- длина продольной волны в полуплоскости.
Решение краевой задачи сведено к граничному интегральному уравнению (ГИУ) вида:
![]()
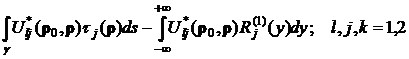 (2)
(2)
относительно неизвестного вектора перемещений ![]() ,
, ![]() на
на ![]() . Здесь
. Здесь ![]() ,
, ![]() - матрицы фундаментальных решений в перемещениях и напряжениях [7,8] для полуплоскости со свободной границей при действии точечного источника колебаний в
- матрицы фундаментальных решений в перемещениях и напряжениях [7,8] для полуплоскости со свободной границей при действии точечного источника колебаний в ![]() .
.
Для фундаментальных решений на основе принципа суперпозиции использовано представление:
![]() , (3)
, (3)
где ![]() - поле точечного источника колебаний интенсивности
- поле точечного источника колебаний интенсивности ![]() в плоскости,
в плоскости, ![]() - поле симметрично расположенного относительно границы
- поле симметрично расположенного относительно границы ![]() источника интенсивности
источника интенсивности ![]() , а
, а ![]() - поле отраженных от
- поле отраженных от ![]() волн.
волн.
Вычисление функций ![]() и
и ![]() в виде набора функций Ханкеля является легко реализуемой задачей. Для поля отраженных волн
в виде набора функций Ханкеля является легко реализуемой задачей. Для поля отраженных волн ![]() ,
, ![]() , имеем представление в виде интеграла Фурье [9]:
, имеем представление в виде интеграла Фурье [9]:
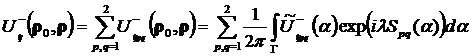 (4)
(4)
![]()
![]()
где, ![]() - амплитудные функции, не содержащие больших параметров.
- амплитудные функции, не содержащие больших параметров.
В случае принятого условия (1) для (4) применим метод стационарной фазы [10] для большого параметра ![]() . В частности получим
. В частности получим
![]() (5)
(5)
![]() ,
, 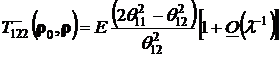
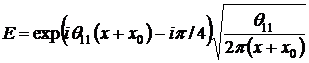 .
.
Дальнейшее исследование задачи осуществлено на основе метода граничных элементов. Участок границы полости в одну длину волны разбивался на 20 элементов. Решение системы линейных алгебраических уравнений осуществлялось методом итераций. В качестве примера на рис. 2 приведены амплитуды радиального и тангенциального перемещений на границе круговой полости в двухслойной полуплоскости в зависимости от угла ![]() при
при ![]() и параметрах задачи:
и параметрах задачи: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() МПа. На рис. 3 отражен характер концентрации напряжений
МПа. На рис. 3 отражен характер концентрации напряжений ![]() на поверхности полости, полученных численным дифференцированием соответствующих поверхностных смещений.
на поверхности полости, полученных численным дифференцированием соответствующих поверхностных смещений.
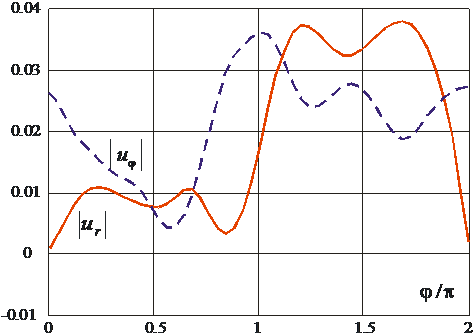
Рис. 2
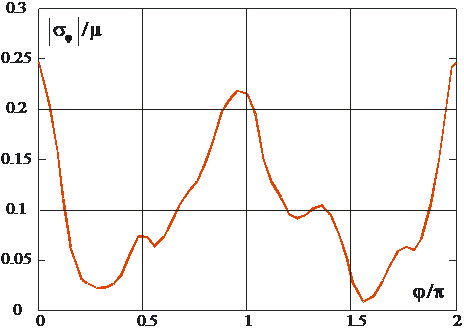
Рис. 3
Литература:
- Гузь, А.Н. Дифракция упругих волн [Текст]: Монография / Гузь, А.Н., Кубенко В.Д., Черевко М.А. -Киев: Наук.думка, 1978. –308 с.
- Ляпин А.А. Возбуждение волн в слоистом полупространстве со сферической полостью [Текст] // Изв. АН СССР, МТТ. –1991. –№3. –C.76-81.
- R.A. Roberts Elastodynamic scattering by a surface-breaking void // J.Acoust.Soc.Am. –1989. –85, 2. – P.561-566.
- Ляпин А.А. О возбуждении волн в слоистой среде с локальным дефектом [Текст] // ПМТФ. –1994. –Т.35. –№.5. –C.87-91.
- Gautesen A.K. Asymptotic solution to the crack-opening displacement integral equations for the scattering of plane waves by cracks. I. The symmetric problem. // J.Acoust. Soc. Amer. -1990. -87, N3. -P.937-942.
- Ляпин А.А., Селезнев М.Г. К построению решений динамических задач для слоистых сред нерегулярной структуры [Текст] // Экологический вестник научных центров ЧЭС, №2, 2006. –С. 37-39.
- Кадомцев М.И., Ляпин А.А., Селезнев М.Г. Исследование динамики заглубленных фундаментов методами граничных и конечных элементов [Текст] // Строительная механика и расчет сооружений. – 2010. – № 3. – С.61–64.
- Кадыров Р.Р., Ляпин А.А. Особенности возбуждения слоистых сред внутренними источниками колебаний [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2009/250 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Кадомцев М.И., Ляпин А.А., Тимофеев С.И. К вопросам построения эффективных алгоритмов расчета системы «сооружение-грунт» [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2009/250 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Федорюк, М.В. Асимптотика: интегралы и ряды [Текст]: Монография / М.В. Федорюк. - М.: Наука, 1987. – 544 с.